Rozwiązanie
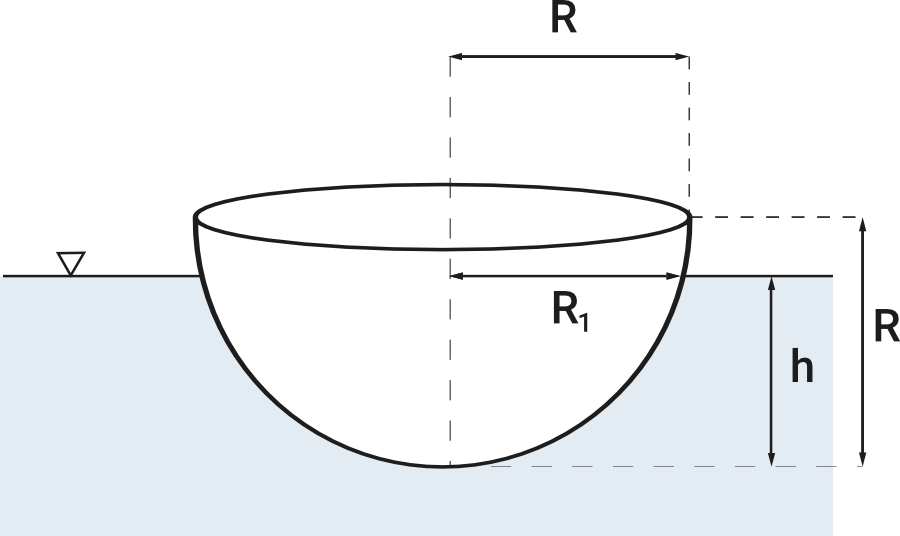
1. Wyznaczyć wartość promienia pływania \(R_1\)
Z równania okręgu o środku w punkcie z=R otrzymamy:
\begin{aligned} &r^2+(z-R)^2=R^2\\ &r(z)=\sqrt{R^2-(z-R)^2}=\sqrt{2 R \cdot z-z^2}\\ &R_1=r(h)=\sqrt{2 R \cdot h-h^2}=1.3 m \end{aligned}2. Wyznaczyć wartość momentu bezwładności powierzchni pływania
\begin{aligned} I_x=\frac{\pi \cdot R_1^4}{4}=2.243 \mathrm{~m}^4 \end{aligned}3. Wyznaczyć objętość części zanurzonej pływającego ciała
Istnieje wzór na objętość odcinka kuli, ale osobiście nie jestem wielkim fanem uczenia się go na pamięć:
Alternatywą jest obliczenia tej objętości ze wzoru całkowego dla figur obrotowych:
Jak widać wynik końcowy wychodzi identyczny :-)
4. Określić gęstość materiału z którego wykonana jest półkula
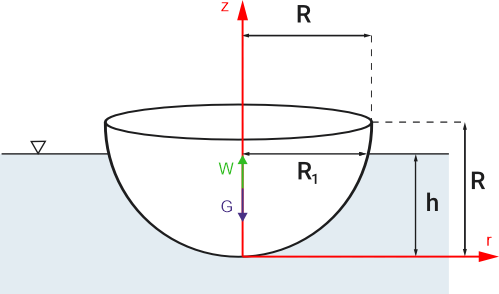
Z prawa Archimedesa oraz warunku równowagi
\begin{aligned} & G=W \\ & \rho_m \cdot g \cdot \frac{1}{2} \frac{4}{3} \pi \cdot R^3=\rho_w \cdot g \cdot V_z \\ & \rho_m=\frac{\rho_w \cdot g \cdot V_z}{g \cdot \frac{1}{2} \frac{4}{3} \pi \cdot R^3}=312.5 \frac{\mathrm{kg}}{\mathrm{m}^3} \end{aligned}