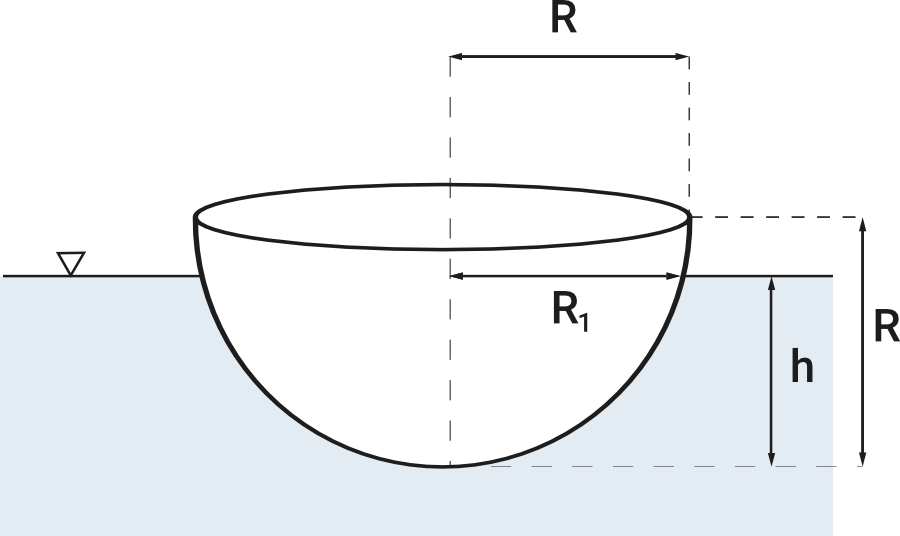
1. Déterminer la valeur du rayon de flottaison \(R_1\)

À partir de l'équation du cercle avec son centre en \(R\), nous obtenons:

\begin{aligned} &r^2+(z-R)^2=R^2\\ &r(z)=\sqrt{R^2-(z-R)^2}=\sqrt{2 R \cdot z-z^2}\\ &R_1=r(h)=\sqrt{2 R \cdot h-h^2}=1.3 m \end{aligned}

2. Déterminer la valeur du moment d'inertie de la surface de flottaison

\begin{aligned} I_x=\frac{\pi \cdot R_1^4}{4}=2.243 \mathrm{~m}^4 \end{aligned}

3. Déterminer le volume de la partie immergée du corps flottant

Il existe une formule pour le volume d'un segment de sphère, mais personnellement je ne suis pas un grand fan de l'apprendre par cœur:

\begin{aligned} V_z=\frac{\pi \cdot h^2}{3}(3 R-h)=2.209 \mathrm{~m}^3 \end{aligned}

Une alternative consiste à calculer ce volume à partir de la formule intégrale pour les figures de révolution:

\begin{aligned} V_z=\pi \int_0^h 2 R \cdot z-z^2 \mathrm{~d} z=2.209 \mathrm{~m}^3 \end{aligned}

Comme on peut le voir, le résultat final est identique :-)

4. Déterminer la densité du matériau à partir duquel la demi-sphère est fabriquée

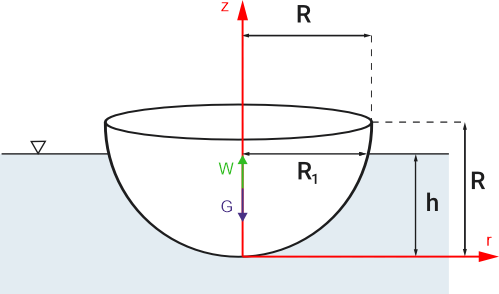
En utilisant la loi d'Archimède et la condition d'équilibre

\begin{aligned} & G=W \\ & \rho_m \cdot g \cdot \frac{1}{2} \frac{4}{3} \pi \cdot R^3=\rho_w \cdot g \cdot V_z \\ & \rho_m=\frac{\rho_w \cdot g \cdot V_z}{g \cdot \frac{1}{2} \frac{4}{3} \pi \cdot R^3}=312.5 \frac{\mathrm{kg}}{\mathrm{m}^3} \end{aligned}