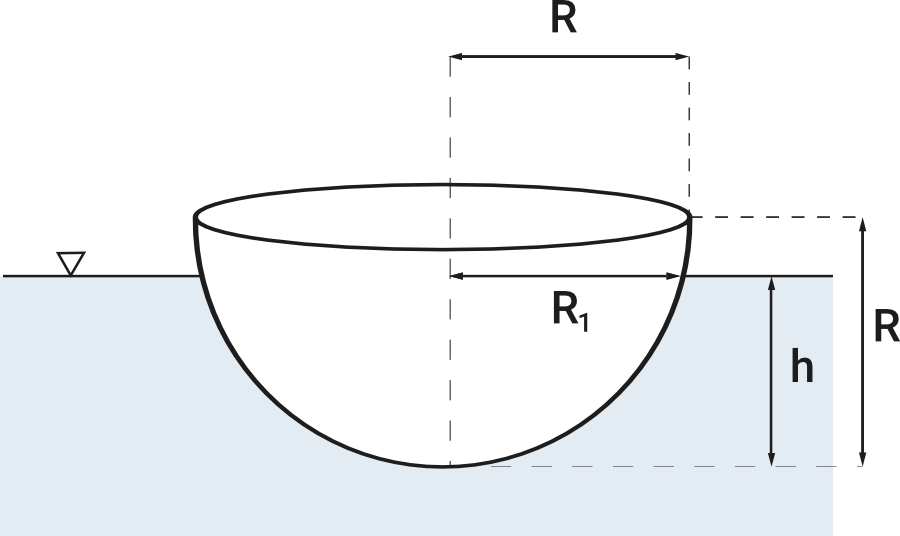
1. Determinar el valor del radio de flotación \(R_1\)

De la ecuación de un círculo con centro en el punto \(z=R\), obtenemos:

\begin{aligned} &r^2+(z-R)^2=R^2\\ &r(z)=\sqrt{R^2-(z-R)^2}=\sqrt{2 R \cdot z-z^2}\\ &R_1=r(h)=\sqrt{2 R \cdot h-h^2}=1.3 m \end{aligned}

2. Determinar el valor del momento de inercia del área de flotación

\begin{aligned} I_x=\frac{\pi \cdot R_1^4}{4}=2.243 \mathrm{~m}^4 \end{aligned}

3. Determinar el volumen de la parte sumergida del cuerpo flotante

Existe una fórmula para el volumen de un segmento de una esfera, pero personalmente no soy fanático de aprenderla de memoria:

\begin{aligned} V_z=\frac{\pi \cdot h^2}{3}(3 R-h)=2.209 \mathrm{~m}^3 \end{aligned}

Una alternativa es calcular este volumen usando una fórmula integral para sólidos de revolución:

\begin{aligned} V_z=\pi \int_0^h 2 R \cdot z-z^2 \mathrm{~d} z=2.209 \mathrm{~m}^3 \end{aligned}

Como se puede ver, el resultado final es el mismo :-)

4. Determinar la densidad del material del que está hecho la semiesfera

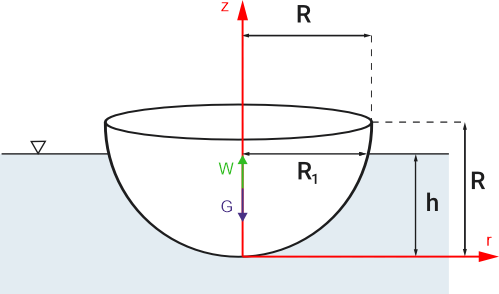
Usando la ley de Arquímedes y la condición de equilibrio

\begin{aligned} & G=W \\ & \rho_m \cdot g \cdot \frac{1}{2} \frac{4}{3} \pi \cdot R^3=\rho_w \cdot g \cdot V_z \\ & \rho_m=\frac{\rho_w \cdot g \cdot V_z}{g \cdot \frac{1}{2} \frac{4}{3} \pi \cdot R^3}=312.5 \frac{\mathrm{kg}}{\mathrm{m}^3} \end{aligned}