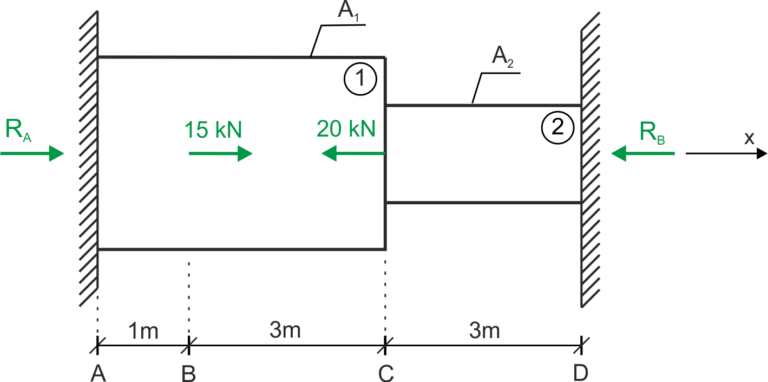
Calcul des réactions
Condition d'équilibre \begin{aligned} &\sum X=0 \\ &R_{A}+15-20-R_{B}=0 \\ \end{aligned} Condition géométrique \begin{aligned} &\Delta l_{c}=0 \\ &\Delta l_{A B}+\Delta l_{B C}+\Delta l_{C D}=0 \\ &\Delta l=\frac{N \cdot l}{E \cdot A} \end{aligned} Décomposition des forces normales sur les tronçons caractéristiques \begin{aligned} &N_{AB}=R_{A}\\ &N_{BC}=R_{A}+15\\ &N_{CD}=R_{A} + 15 - 20=R_{A} - 5\\ \end{aligned} Résolution de la condition géométrique \begin{aligned} &\frac{R_{A}\cdot 1}{E_{1}\cdot A_{1}}+\frac{(R_{A}+15)\cdot 3}{E_{1}\cdot A_{1}}+\frac{(R_{A}-5)\cdot 3}{E_{2}\cdot A_{2}}=0\\ &\frac{R_{A}}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}+45}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}-15}{2E_{1}\cdot A_{2}}=0 & |\cdot E_{1}\cdot A_{2}\\ &\frac{1}{2}R_{A}+\frac{3}{2}R_{A}+22,5+\frac{3}{2}R_{A}-7,5=0\\ &3,5R_{A}=-15\\ &R_{A}=-4,286 \ kN\\ &R_{A}+15 - 20 - R_{B}=0\\ &R_{B}=-9,286 \ kN\\ \end{aligned} 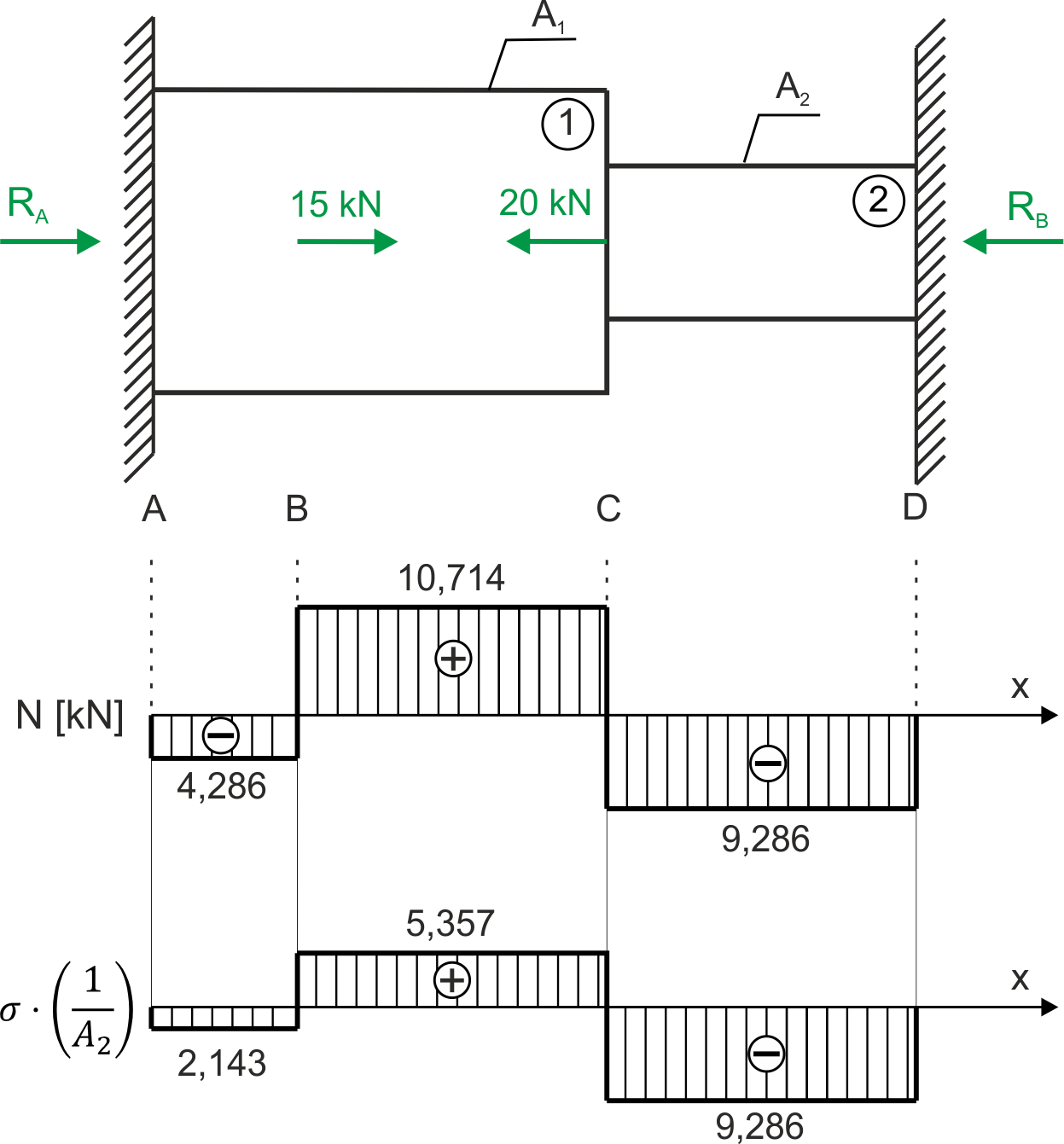Après calcul des réactions RA, les forces sur les tronçons ont les valeurs suivantes: \begin{aligned} &N_{AB}=R_{A}=-4,286 \ kN\\ &N_{BC}=R_{A}+15=10,714 \ kN\\ &N_{CD}=R_{A}+15-20=R_{A}-5=-9,286 \ kN \\ \end{aligned} Décomposition des contraintes normales sur les tronçons caractéristiques \begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{AB}=\frac{-4,286}{A_{1}}=\frac{-4,286}{2A_{2}}=-2,143\cdot\frac{1}{A_{2}}\\ &\sigma_{BC}=\frac{10,714}{A_{1}}=\frac{10,714}{2A_{2}}=5,357\cdot\frac{1}{A_{2}}\\ &\sigma_{CD}=\frac{9,286}{A_{2}}=9,286\cdot\frac{1}{A_{2}}\\ \end{aligned} Graphiques