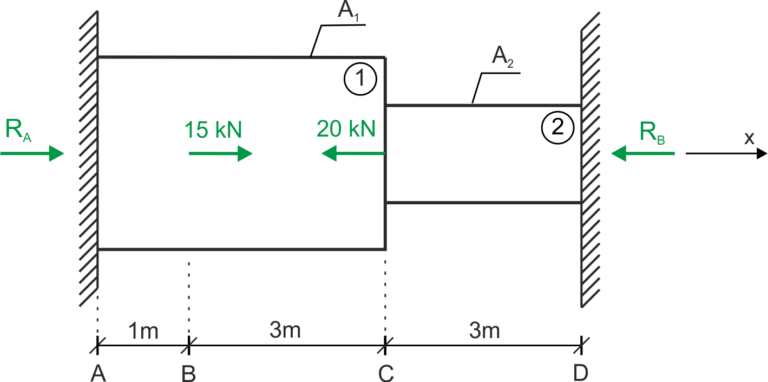
Solución
Cálculo de las reacciones
Condición de estática
\begin{aligned}
&\sum X=0 \\
&R_{A}+15-20-R_{B}=0 \\
\end{aligned}
Condición geométrica
\begin{aligned}
&\Delta l_{c}=0 \\
&\Delta l_{A B}+\Delta l_{B C}+\Delta l_{C D}=0 \\
&\Delta l=\frac{N \cdot l}{E \cdot A}
\end{aligned}
Desglose de las fuerzas normales en los intervalos característicos
\begin{aligned}
&N_{AB}=R_{A}\\
&N_{BC}=R_{A}+15\\
&N_{CD}=R_{A} + 15 - 20=R_{A} - 5\\
\end{aligned}
Resolución de la condición geométrica
\begin{aligned}
&\frac{R_{A}\cdot 1}{E_{1}\cdot A_{1}}+\frac{(R_{A}+15)\cdot 3}{E_{1}\cdot A_{1}}+\frac{(R_{A}-5)\cdot 3}{E_{2}\cdot A_{2}}=0\\
&\frac{R_{A}}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}+45}{E_{1}\cdot 2A_{2}}+\frac{3R_{A}-15}{2E_{1}\cdot A_{2}}=0 & |\cdot E_{1}\cdot A_{2}\\
&\frac{1}{2}R_{A}+\frac{3}{2}R_{A}+22,5+\frac{3}{2}R_{A}-7,5=0\\
&3,5R_{A}=-15\\
&R_{A}=-4,286 \ kN\\
&R_{A}+15 - 20 - R_{B}=0\\
&R_{B}=-9,286 \ kN\\
\end{aligned}
Una vez calculadas las reacciones RA, las fuerzas en los intervalos tienen los siguientes valores:
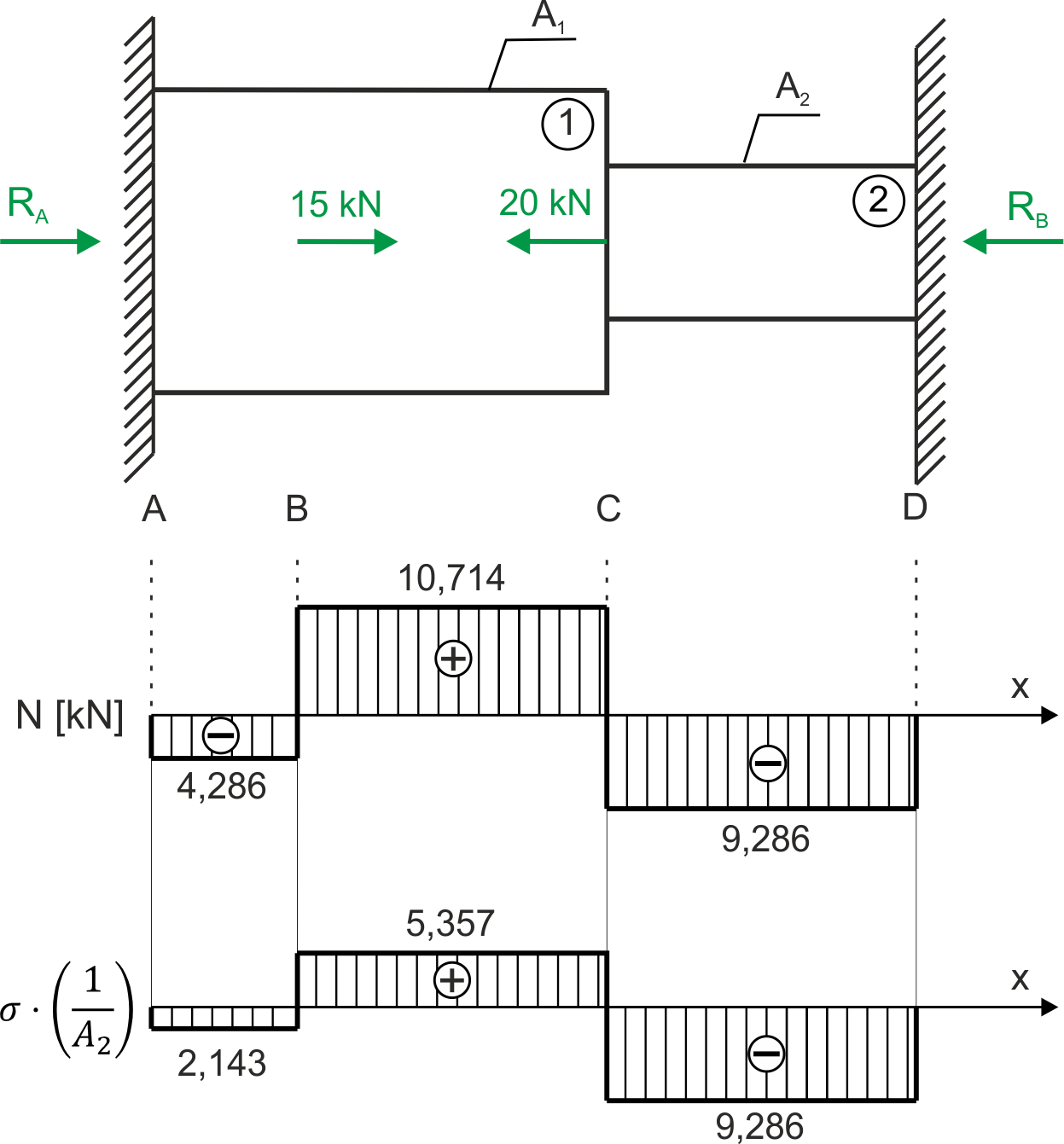
\begin{aligned}
&N_{AB}=R_{A}=-4,286 \ kN\\
&N_{BC}=R_{A}+15=10,714 \ kN\\
&N_{CD}=R_{A}+15-20=R_{A}-5=-9,286 \ kN \\
\end{aligned}
Desglose de las tensiones normales en los intervalos característicos
\begin{aligned}
&\sigma=\frac{N}{A}\\
&\sigma_{AB}=\frac{-4,286}{A_{1}}=\frac{-4,286}{2A_{2}}=-2,143\cdot\frac{1}{A_{2}}\\
&\sigma_{BC}=\frac{10,714}{A_{1}}=\frac{10,714}{2A_{2}}=5,357\cdot\frac{1}{A_{2}}\\
&\sigma_{CD}=\frac{9,286}{A_{2}}=9,286\cdot\frac{1}{A_{2}}\\
\end{aligned}
Gráficos

Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.