Solution
Avant de commencer cet exemple, veuillez lire une brève introduction théorique et une procédure pour la méthode des forces (lien ci-dessous).
PROCÉDURE - Méthode des forces
SSN=4-3=1
Configuration de base de la méthode des forces (UPMS)
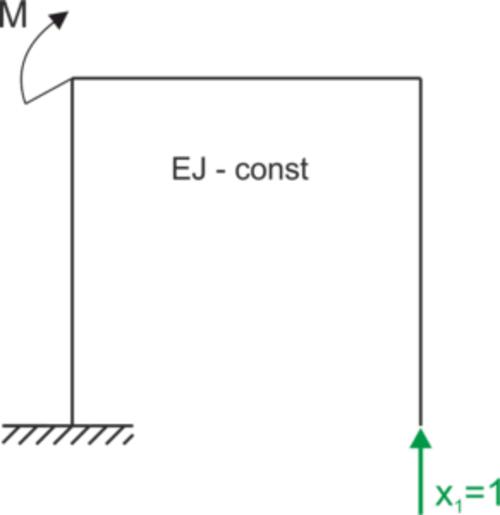
État x1=1
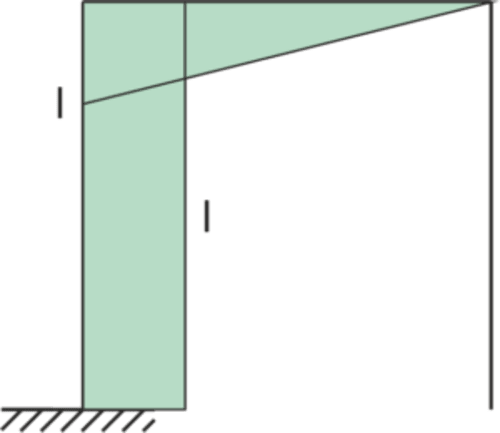
Graphique M1
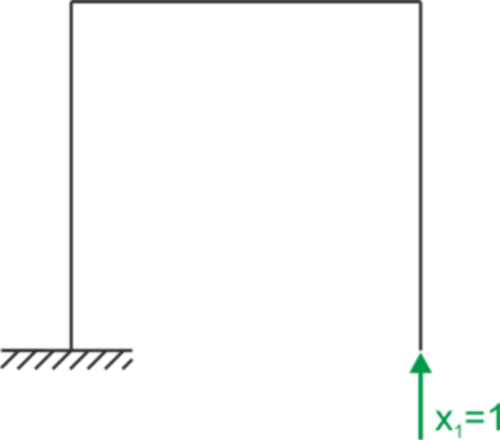
État P

Graphique Mp

Équation canonique de la méthode des forces
\begin{aligned} &\delta_{11}\cdot x_1+\delta_{1p}=0\\ \end{aligned}Intégration graphique - Pages 2, 4 et 5 du fichier
\begin{aligned} \delta_{11}=\\ \end{aligned} \begin{aligned} =\frac{1}{EI}(l\cdot l\cdot l+\frac{1}{3}\cdot l\cdot l\cdot l)=\frac{4l^3}{3EI}\\ \end{aligned}
\begin{aligned} \delta_{1p}= \end{aligned}
\begin{aligned} =\frac{1}{EI}(l\cdot l\cdot l+\frac{1}{3}\cdot l\cdot l\cdot l)=\frac{4l^3}{3EI}\\ \end{aligned}
\begin{aligned} \delta_{1p}= \end{aligned}
 \begin{aligned} =\frac{1}{EI}(-M\cdot l\cdot l)=-\frac{Ml^2}{EI}\\ \end{aligned}
\begin{aligned} =\frac{1}{EI}(-M\cdot l\cdot l)=-\frac{Ml^2}{EI}\\ \end{aligned}
Résolution de l'équation canonique
\begin{aligned} &\frac{4l^3}{3EI}\cdot x_1-\frac{Ml^2}{EI}=0\\ &x_1=\frac{3M}{4l}\\ \end{aligned}Calcul des autres réactions
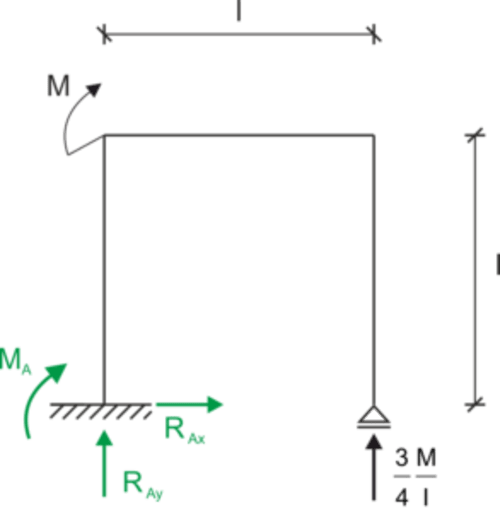 \begin{aligned} &\sum x=0 \Rightarrow R_{Ax}=0\\ &\sum y=0 \Rightarrow R_{Ay}=-\frac{3M}{4l}\\ &\sum M_A=0 \Rightarrow M_A=-\frac{1}{4}M\\ \end{aligned}
\begin{aligned} &\sum x=0 \Rightarrow R_{Ax}=0\\ &\sum y=0 \Rightarrow R_{Ay}=-\frac{3M}{4l}\\ &\sum M_A=0 \Rightarrow M_A=-\frac{1}{4}M\\ \end{aligned}
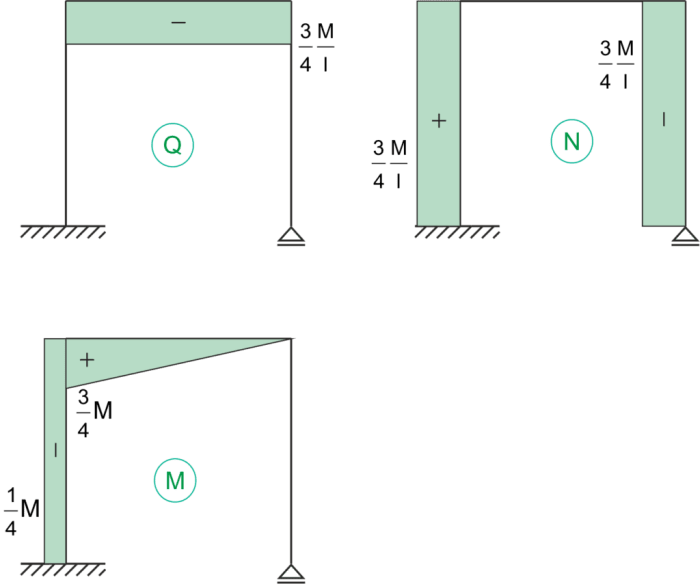
Graphiques finaux pour les forces internes