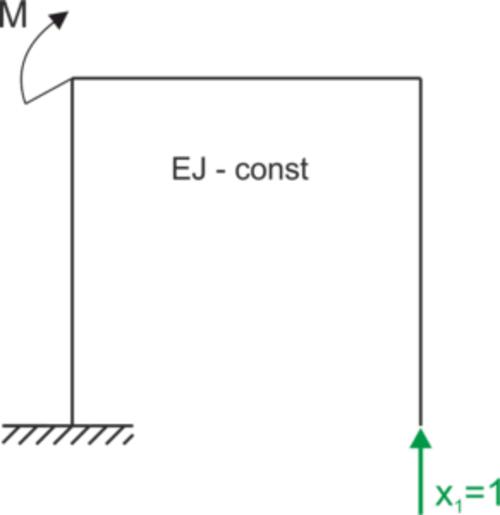
SSN=4-3=1

Basic system of the force method (BSFM)

State x1=1

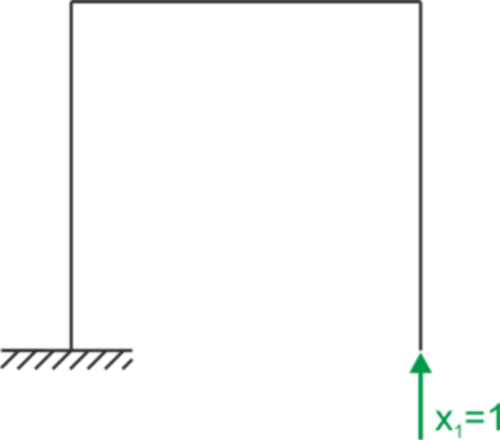
M1 Chart

State P

Mp Chart

Canonical equation of the force method

\begin{aligned} &\delta_{11}\cdot x_1+\delta_{1p}=0\\ \end{aligned}

Graphical integration - page 2, 4, and 5 of the file

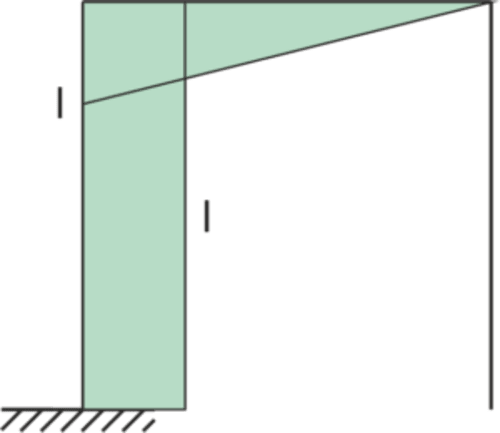
\begin{aligned} \delta_{11}=\\ \end{aligned} \begin{aligned} =\frac{1}{EI}(l\cdot l\cdot l+\frac{1}{3}\cdot l\cdot l\cdot l)=\frac{4l^3}{3EI}\\ \end{aligned} \begin{aligned} \delta_{1p}= \end{aligned} \begin{aligned} =\frac{1}{EI}(-M\cdot l\cdot l)=-\frac{Ml^2}{EI}\\ \end{aligned}

Solution to the canonical equation

\begin{aligned} &\frac{4l^3}{3EI}\cdot x_1-\frac{Ml^2}{EI}=0\\ &x_1=\frac{3M}{4l}\\ \end{aligned}

Calculation of the remaining reactions

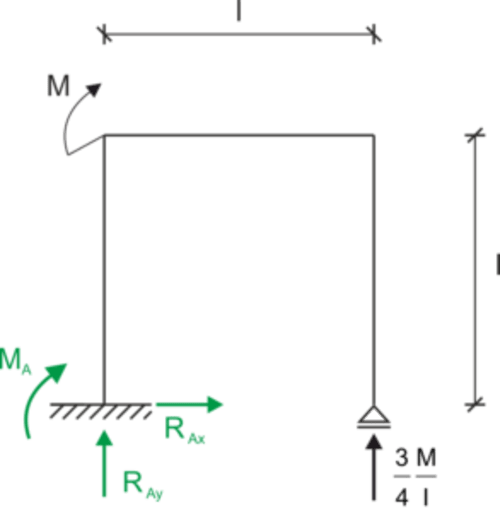\begin{aligned} &\sum x=0 \Rightarrow R_{Ax}=0\\ &\sum y=0 \Rightarrow R_{Ay}=-\frac{3M}{4l}\\ &\sum M_A=0 \Rightarrow M_A=-\frac{1}{4}M\\ \end{aligned}

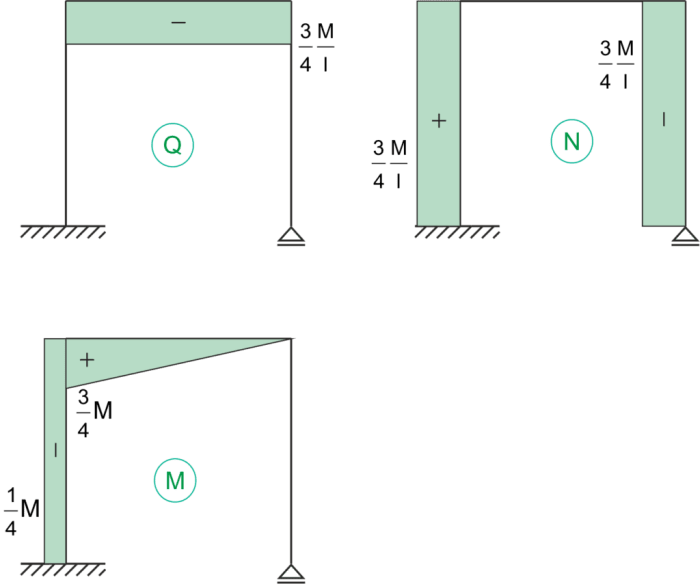
Final internal force charts