Solución
Antes de comenzar este ejemplo, lea una breve Introducción teórica y el procedimiento para el método de fuerzas (enlace a continuación).
PROCEDIMIENTO - Método de fuerzas
SSN=4-3=1
Configuración básica del método de fuerzas (CBMF)
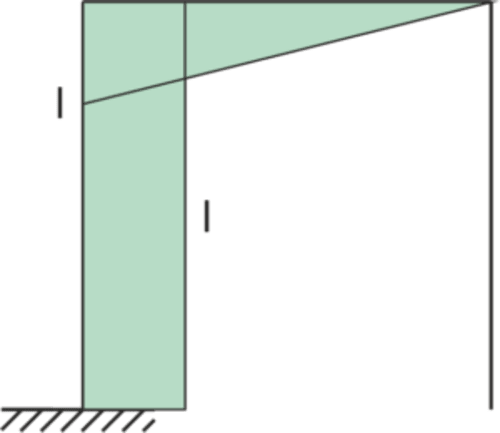
Estado x1=1
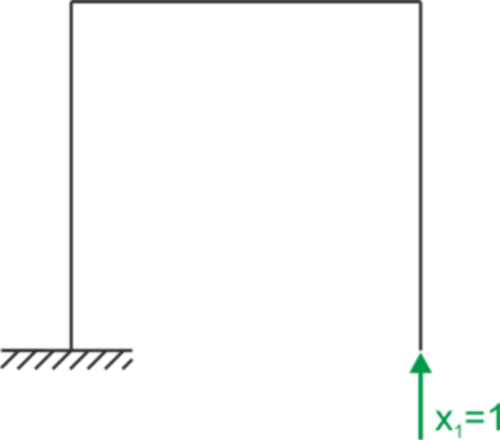
Gráfico M1
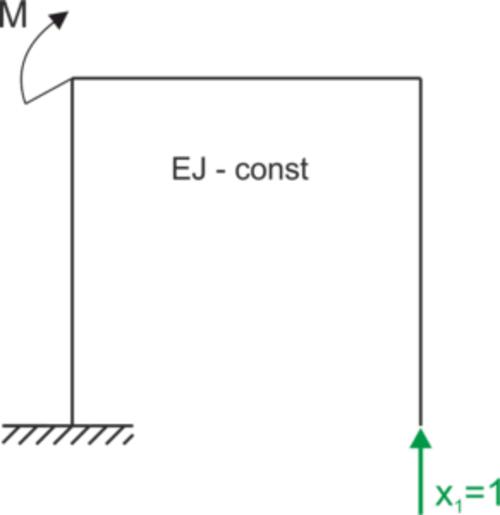
Estado P

Gráfico Mp

Ecuación canónica del método de fuerzas
\begin{aligned} &\delta_{11}\cdot x_1+\delta_{1p}=0\\ \end{aligned}Integración gráfica - página 2, 4 y 5 del archivo
\begin{aligned} \delta_{11}=\\ \end{aligned} \begin{aligned} =\frac{1}{EI}(l\cdot l\cdot l+\frac{1}{3}\cdot l\cdot l\cdot l)=\frac{4l^3}{3EI}\\ \end{aligned}
\begin{aligned} \delta_{1p}= \end{aligned}
\begin{aligned} =\frac{1}{EI}(l\cdot l\cdot l+\frac{1}{3}\cdot l\cdot l\cdot l)=\frac{4l^3}{3EI}\\ \end{aligned}
\begin{aligned} \delta_{1p}= \end{aligned}
 \begin{aligned} =\frac{1}{EI}(-M\cdot l\cdot l)=-\frac{Ml^2}{EI}\\ \end{aligned}
\begin{aligned} =\frac{1}{EI}(-M\cdot l\cdot l)=-\frac{Ml^2}{EI}\\ \end{aligned}
Solución de la ecuación canónica
\begin{aligned} &\frac{4l^3}{3EI}\cdot x_1-\frac{Ml^2}{EI}=0\\ &x_1=\frac{3M}{4l}\\ \end{aligned}Cálculo de las demás reacciones
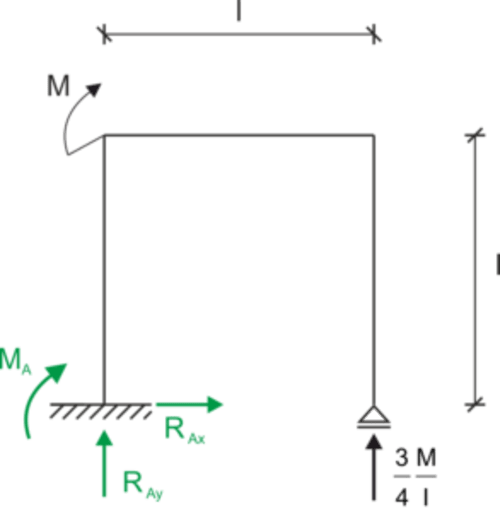 \begin{aligned} &\sum x=0 \Rightarrow R_{Ax}=0\\ &\sum y=0 \Rightarrow R_{Ay}=-\frac{3M}{4l}\\ &\sum M_A=0 \Rightarrow M_A=-\frac{1}{4}M\\ \end{aligned}
\begin{aligned} &\sum x=0 \Rightarrow R_{Ax}=0\\ &\sum y=0 \Rightarrow R_{Ay}=-\frac{3M}{4l}\\ &\sum M_A=0 \Rightarrow M_A=-\frac{1}{4}M\\ \end{aligned}
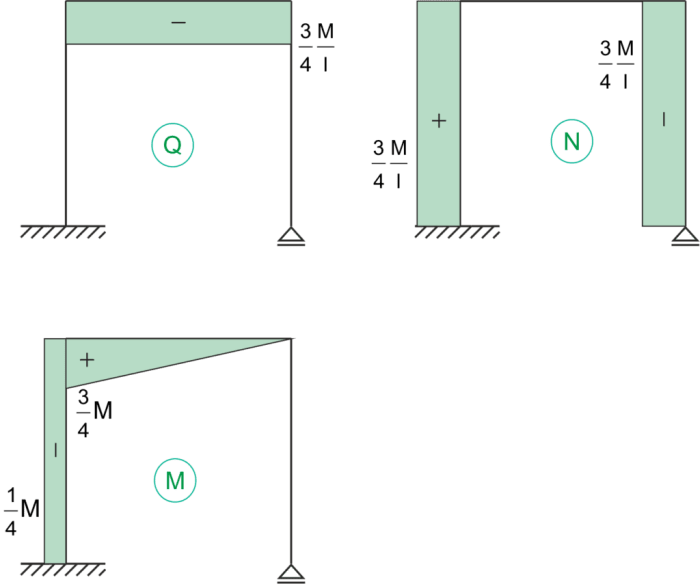
Gráficos finales de las fuerzas internas