Rozwiązanie
Zobacz wstęp teoretyczny do metody równoważenia węzłów! W tym również nakierowanie na więcej zadań i materiałów z tego tematu!



Będą to pręty 4 i 6 z trzeciego twierdzenia o prętach zerowych oraz pręt numer 7, z drugiego twierdzenia
Możemy zacząć w zasadzie albo od węzła A albo od węzła (7-9).
Zacznijmy od węzła A (1-3).



W tym momencie trzy pręty określiliśmy na początku jako zerowe, kolejne cztery policzyliśmy z równowagi dwóch węzłow, czyli mamy 7 z 9 prętów. Pozostał pręt nr 9 i pręt nr 2.
Z drugiego twierdzenia o prętach zerowych wynika w zasadzie dodatkowa zasada - jeżeli siła obciąża węzeł w taki sposób, że jej kierunek jest współliniowy z jednym z prętów i żadna inna siła nie daje się rzutować na tą prostą, to siła w pręcie przekazuje się współliniowo.
Spójrzmy na rysunek poniżej, który prezentuje wykres sił normalnych.
Taką sytuację mamy w węzłach zaznaczonych na rysunku.

Wykres sił normalnych, znakowanie:
DODATNIE

UJEMNE

Przykład
Treść
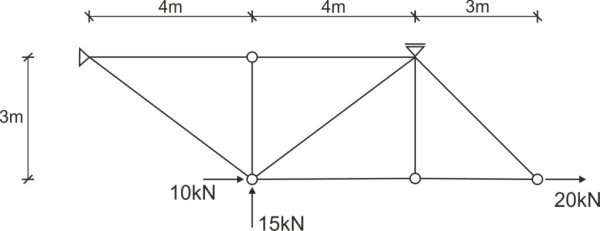
Dla danej kratownicy wskazać pręty zerowe oraz wyznaczyć siły we wszystkich prętach metodą równoważenia węzłów.

Rozwiązanie
Krok 1
Ponumerowanie prętów, ewentualne oznaczenie węzłów, zaznaczenie reakcji podporowych.
Krok 2
Rozpisanie równań równowagi statycznej i obliczenie reakcji podporowych.
Krok 3
Wyznaczamy pręty zerowe.Będą to pręty 4 i 6 z trzeciego twierdzenia o prętach zerowych oraz pręt numer 7, z drugiego twierdzenia
Krok 4
Robimy równowagi węzłów.Możemy zacząć w zasadzie albo od węzła A albo od węzła (7-9).
Zacznijmy od węzła A (1-3).

Zapisujemy równania równowagi statycznej dla tego węzła.
Możemy zapisać sumę rzutów na oś "x" oraz "y"
Analogicznie robimy wycięcie węzła (3-4-5-8).

W tym momencie trzy pręty określiliśmy na początku jako zerowe, kolejne cztery policzyliśmy z równowagi dwóch węzłow, czyli mamy 7 z 9 prętów. Pozostał pręt nr 9 i pręt nr 2.
Z drugiego twierdzenia o prętach zerowych wynika w zasadzie dodatkowa zasada - jeżeli siła obciąża węzeł w taki sposób, że jej kierunek jest współliniowy z jednym z prętów i żadna inna siła nie daje się rzutować na tą prostą, to siła w pręcie przekazuje się współliniowo.
Spójrzmy na rysunek poniżej, który prezentuje wykres sił normalnych.
Taką sytuację mamy w węzłach zaznaczonych na rysunku.

Wykres sił normalnych, znakowanie:
DODATNIE

UJEMNE

Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: