Solution
Découvrez l'introduction théorique à la méthode d'équilibrage des nœuds! Cela inclut également des conseils pour plus d'exercices et de matériel sur ce sujet!


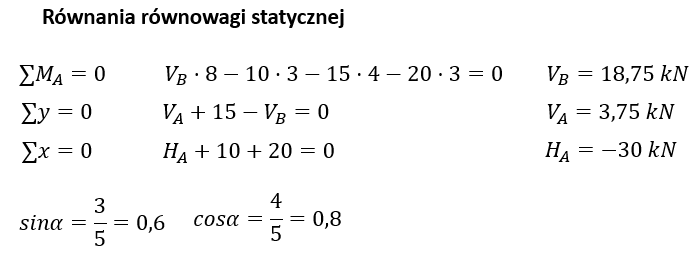
Il s'agit des barres 4 et 6 avec le troisième théorème des barres nulles, ainsi que la barre 7 avec le deuxième théorème
Nous pouvons commencer par le nœud A ou le nœud (7-9).
Commençons par le nœud A (1-3).



À ce stade, nous avons identifié trois barres comme étant nulles, nous avons calculé quatre autres à partir de l'équilibre de deux nœuds, ce qui nous donne 7 des 9 barres. Restent les barres 9 et 2.
Le deuxième théorème des barres nulles implique essentiellement une règle supplémentaire: si une force appliquée sur un nœud est telle que sa direction est colinéaire avec l'une des barres et qu'aucune autre force ne peut être projetée sur cette ligne, alors la force dans la barre est colinéaire.
Regardons l'image ci-dessous, qui montre le graphique de forces normales.
Nous avons cette situation dans les nœuds indiqués sur l'image.

Graphique des forces normales, marquage:

Exemple
Contenu
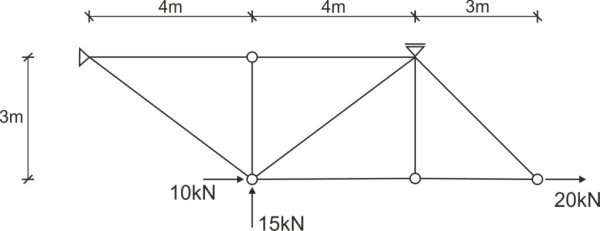
Pour une treillis donnée, identifier les barres nulles et déterminer les forces dans toutes les barres à l'aide de la méthode d'équilibrage des nœuds.

Solution
Étape 1
Numérotez les barres, marquez éventuellement les nœuds, indiquez les réactions d'appui.
Étape 2
Écrivez les équations d'équilibre statique et calculez les réactions d'appui.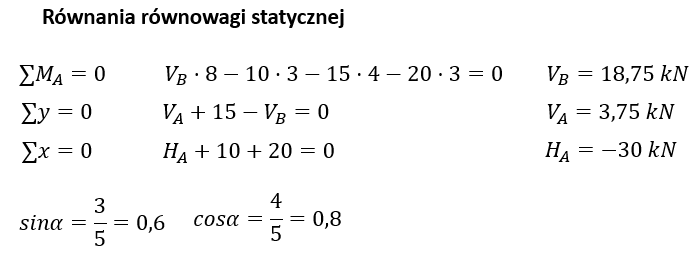
Étape 3
Déterminez les barres nulles.Il s'agit des barres 4 et 6 avec le troisième théorème des barres nulles, ainsi que la barre 7 avec le deuxième théorème
Étape 4
Équilibrez les nœuds.Nous pouvons commencer par le nœud A ou le nœud (7-9).
Commençons par le nœud A (1-3).

Écrivons les équations d'équilibre statique pour ce nœud.
Nous pouvons écrire la somme des projections sur l'axe "x" et "y"
De même, coupes le nœud (3-4-5-8).

À ce stade, nous avons identifié trois barres comme étant nulles, nous avons calculé quatre autres à partir de l'équilibre de deux nœuds, ce qui nous donne 7 des 9 barres. Restent les barres 9 et 2.
Le deuxième théorème des barres nulles implique essentiellement une règle supplémentaire: si une force appliquée sur un nœud est telle que sa direction est colinéaire avec l'une des barres et qu'aucune autre force ne peut être projetée sur cette ligne, alors la force dans la barre est colinéaire.
Regardons l'image ci-dessous, qui montre le graphique de forces normales.
Nous avons cette situation dans les nœuds indiqués sur l'image.

Graphique des forces normales, marquage:

Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.