Przykład 1

Wyznaczyć i narysować wykresy sił wewnętrznych.

single-task-hero-img

Rozwiązanie

Wersja YT

Wersja klasyczna

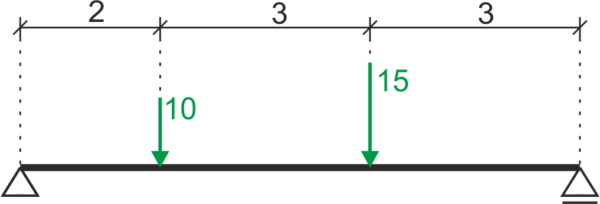
1. Oznaczenie punktów charakterystycznych oraz reakcji na podporach

2. Obliczenie reakcji korzystając z równań równowagi

\begin{aligned} &\sum{X}=0\\ &H_A=0\\ \end{aligned} \begin{aligned} &\sum{M_{A}}=0\\ &10\cdot 2+15\cdot 5-V_{D}\cdot 8=0\\ &V_{D}=11,875 \ kN\\ \end{aligned} \begin{aligned} &\sum{M_{D}}=0\\ &V_{A}\cdot 8-15\cdot 3-10\cdot 6=0\\ &V_{A}=13,125 \ kN\\ \end{aligned} \begin{aligned} &\sum{Y}=0\\ &V_{A}+V_{D}-10-15=0\\ &L=P\\ \end{aligned}

3. Rozpisanie równań sił wewnętrznych w poszczególnych przedziałach zmienności:

a) Przedział AB

\begin{aligned} &Q_{AB}=V_{A}=13,125 kN\\ &M_{AB}=V_{A}\cdot x\\ &M_{A}(0)=0\\ &M_{B}(2)=26,25 kNm\\ \end{aligned}

b )Przedział BC 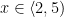x \in{\langle 2,5)}

\begin{aligned} &Q_{BC}=V_{A}-10=3,125\\ &M_{BC}=V_{A}\cdot x-10\cdot (x-2)\\ &M_{B}(2)=26,25 kNm\\ &M_{C}(5)=35,625 kNm\\ \end{aligned}

c) Przedział DC 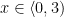x \in{\langle 0,3)}

\begin{aligned} &Q_{DC}=-V_{D}\\ &M_{DC}=V_{D}\cdot x\\ &M_{D(0)}=0\\ &M_{C(3)}=35,625 kNm\\ \end{aligned}

4. Wykresy ostateczne