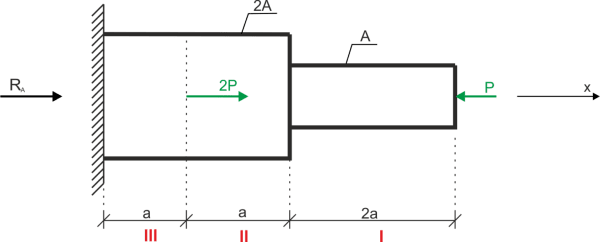
Rozwiązanie
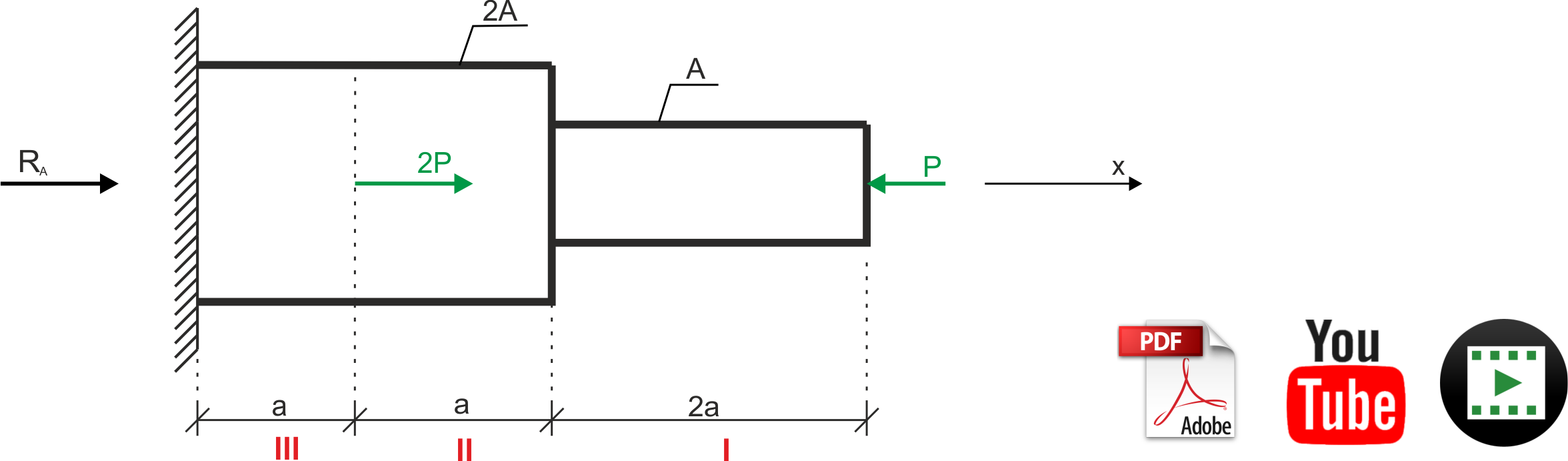
Obliczenie rekacji
\begin{aligned} &\sum X=0 \\ &R_{A}+2 P-P=0 \\ &R_{A}=-P \\ \end{aligned} Zapisanie sił normalnych na przedziałach charakterystycznych
\begin{aligned} &N_{1}=-P=-10 k N \\ &N_{2}=-P=-10 k N \\ &N_{3}=-P+2 P=P=10 k N \\ \end{aligned} Warunek wytrzymałości
\begin{aligned} &\sigma=\left|\frac{N}{A}\right| \leq k_{r}, k_{c} \end{aligned} Ściskanie \begin{aligned} &\frac{10 \cdot 10^{3}}{A} \leq 80 \cdot 10^{6} \\ &A \geq \frac{10 \cdot 10^{3}}{80 \cdot 10^{6}} \\ &A \geq 1,25 \cdot 10^{-4}\left[\mathrm{~m}^{2}\right] \end{aligned}
Rozciąganie
\begin{aligned} &\frac{10 \cdot 10^3}{2 A} \leq 60 \cdot 10^{6} \\ &2 A \geq \frac{10 \cdot 10^{3}}{60 \cdot 10^{6}} \\ &A \geq 8,33 \cdot 10^{-5}=0,833 \cdot 10^{-4}\left[\mathrm{~m}^{2}\right] \end{aligned} Decyduje warunek na rozciąganie. Wymiarowanie średnicy: \begin{aligned} &A \geq 1,25 \cdot 10^{-4} \\ &\frac{\pi d^{2}}{4} \geq 1,25 \cdot 10^{-4} \\ &d \geq \sqrt{\frac{4 \cdot 1,25 \cdot 10^{-4}}{\pi}} \\ &d \geq 0,0126 \\ &d=0,013 \ [m]\\ \end{aligned} Pole przekroju na zwymiarowanej średnicy: \begin{aligned} &A=\frac{\pi \cdot 0,013^{2}}{4}=1,327 \cdot 10^{-4} \end{aligned} Naprężenia na przedziałach charakterystycznych: \begin{aligned} \sigma_{1} &=\frac{N_{1}}{A}=-\frac{10 \cdot 10^{3}}{1,327 \cdot 10^{-4}}=-75,36 \mathrm{MPa} \\ \sigma_{2} &=\frac{N_{2}}{2 A}=-\frac{10 \cdot 10^{3}}{2 \cdot 1,327 \cdot 10^{-4}}=-37,68 \mathrm{MPa} \\ \sigma_{3} &=\frac{N_{3}}{2 A}=\frac{10 \cdot 10^{3}}{2 \cdot 1,327 \cdot 10^{-4}}=37,68 \mathrm{MPa} \end{aligned} Wydłużenia \begin{aligned} &\Delta l=\frac{N \cdot l}{E \cdot A} \\ &\Delta l_{1}=\frac{N_{1} \cdot l_{1}}{E \cdot A}=\frac{-10 \cdot 10^{3} \cdot 2 \cdot 1}{2,1 \cdot 10^{11} \cdot 1,327 \cdot 10^{-4}}=-7,18 \cdot 10^{-4}[\mathrm{~m}]=-7,18 \cdot 10^{-4}[\mathrm{~mm}]=-0,718[\mathrm{~mm}] \\ &\Delta l_{1}=\frac{N_{1} \cdot l_{1}}{E \cdot 2 A}=\frac{-10 \cdot 10^{3} \cdot 1 \cdot 1}{2,1 \cdot 10^{11} \cdot 2 \cdot 1,327 \cdot 10^{-4}}=-1,79 \cdot 10^{-4}[\mathrm{~m}]=-0,179[\mathrm{~mm}] \\ &\Delta l_{1}=\frac{N_{1} \cdot l_{1}}{E \cdot 2 A}=\frac{10 \cdot 10^{3} \cdot 2 \cdot 1}{2,1 \cdot 10^{11} \cdot 2 \cdot 1,327 \cdot 10^{-4}}=1,79 \cdot 10^{-4}[\mathrm{~m}]=0,179[\mathrm{~mm}] \end{aligned} Podsumowanie: \begin{aligned} &N_{1}=10 k N \\ &N_{2}=-10 k N \\ &N_{3}=10 k N \\ &\sigma_{1}=-75,36 \mathrm{MPa} \\ &\sigma_{2}=-37,68 \mathrm{MPa} \\ &\sigma_{3}=37,68 \mathrm{MPa} \\ &\Delta l_{3}=0,179 \mathrm{~mm} \\ &\Delta l_{2}=-0,179 \mathrm{~mm} \\ &\Delta l_{1}=-0,718 \mathrm{~mm} \\ \end{aligned} Przemieszczenia \begin{aligned} &u_{I I I}=\Delta l_{3}=0,179 \mathrm{~mm} \\ &u_{I I}=\Delta l_{3}+\Delta l_{2}=0,179-0,179=0 \mathrm{~mm} \\ &u_{I}=\Delta l_{3}+\Delta l_{2}+\Delta l_{1}=-0,718 \mathrm{~mm} \end{aligned} Wykresy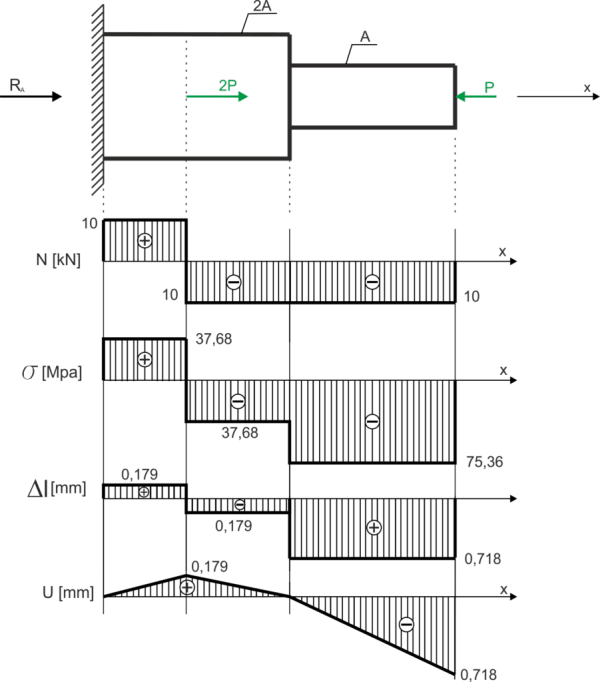
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: