Solution
Pour les curieux, voici le lien vers la solution dans Robot Structural Analysis :
kratownica1.rtd
Exemple de calcul avec commentaire
Contenu
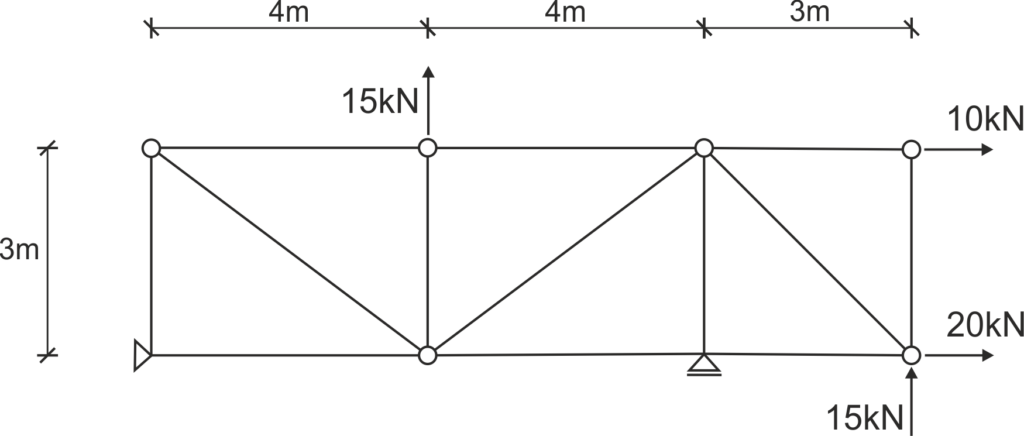
Pour une grille donnée, indiquer les barres nulles et déterminer les forces dans toutes les barres avec la méthode de Ritter.
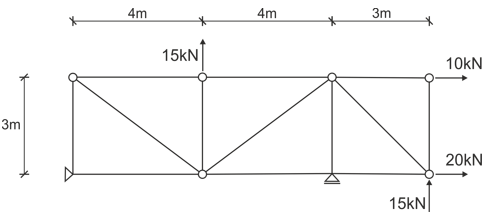
Solution
Étape 1
Numérotez les barres, éventuellement marquez les nœuds, indiquez les réactions d'appui.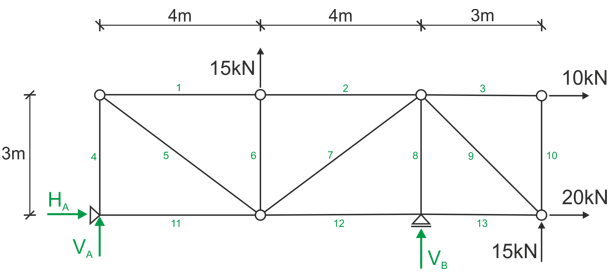
Étape 2
Écrivez les équations d'équilibre statique et calculez les réactions d'appui.
Étape 3
Faites les coupes de Rittera.Nous pouvons commencer de n'importe quelle manière, tant que nous ne coupons pas plus de 3 barres, car c'est le nombre de variables que nous pouvons calculer dans une seule coupe.
Commençons par la coupe des barres 2, 7 et 12 et faisons une vue de gauche.

Écrivons les équations d'équilibre statique.
Les soi-disant points de Ritter sont les points d'intersection des deux inconnues.Cependant, si nous avons seulement deux points de Ritter comme ici, ce n'est pas grave, nous écrivons deux sommes de moments et comme troisième équation, nous pouvons écrire soit la somme des projections sur l'axe "x", soit (mieux) sur "y", car seule l'inconnue N7 entre dans cette équation.
Nous pouvons également écrire la somme des moments dans un autre point, afin de calculer la dernière inconnue, ici le point (3) est déterminé.
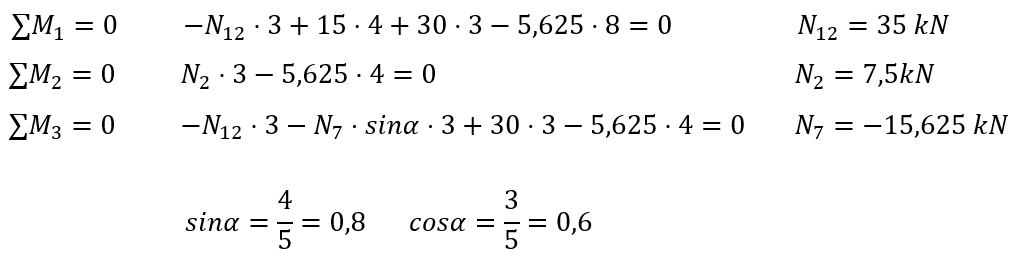
Faisons de même avec l'intersection Rittera des barres 1, 5, 11.
Vue de gauche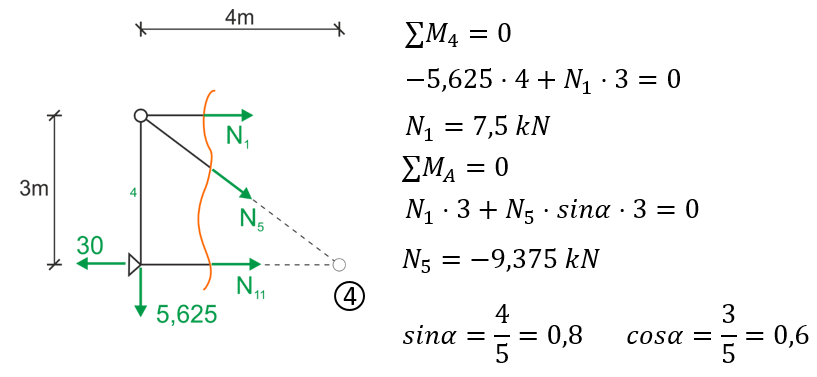
Enfin avec l'intersection Rittera des barres 3, 9, 13.
Vue de droite
Étape 5
Terminer la résolution du problème.Tracer le graphique des forces normales dans les barres déjà calculées.
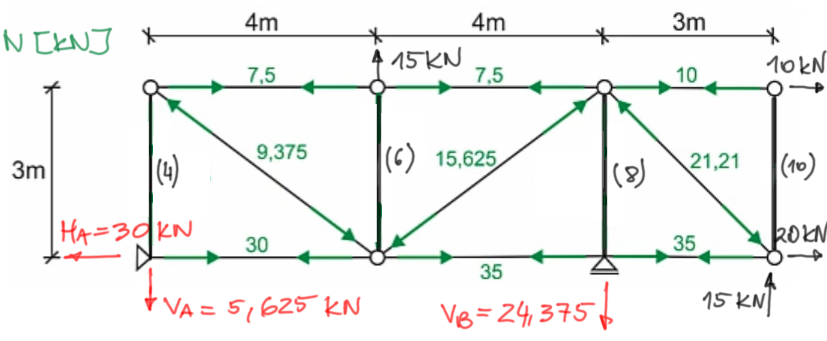 Graphique des forces normales, marquage :
Graphique des forces normales, marquage :
Nous avons calculé les forces pour la plupart des barres (9 sur 13). Il nous reste 4 barres (verticales 4, 6, 8 et 10), nous avons trois options :
- faire d'autres coupes, mais nous avons déjà besoin de quatre intersections distinctes pour calculer ces forces, ce qui est un peu contre-productif.
- faisons l'équilibre des nœuds A, B, (3-10) et (1-2-6) et ajoutons les quatre dernières forces, cela nécessite certainement moins de dessin en coupant un seul nœud que de faire une plus grande coupe,
- remarquons astucieusement que :
1) d'après le deuxième théorème des forces nulles, la barre (10) est nulle,
2) d'après le deuxième théorème,
la règle supplémentaire - si une force charge un nœud de telle manière que sa direction est colinéaire avec l'une des barres et aucune autre force ne peut être projetée sur cette ligne droite, alors la force dans la barre est transmise de manière colinéaire.
Regardons la ceinture inférieure et le nœud B - la force de 35 kN dans la barre horizontale passe de la barre à la barre comme indiqué sur le graphique,
alors que la réaction VB=24,375 kN charge colinéairement la barre (8) - donc elle transmet directement la force de traction sur cette barre (car nous voyons que la réaction VB agit sur la barre (8) en la tendant).
au final, nous connaissons donc la force dans la barre (8)
3) de même, N6=15 kN
4) de même, N4=5,625 kN
Étape 5
Tracer le graphique final des forces normales.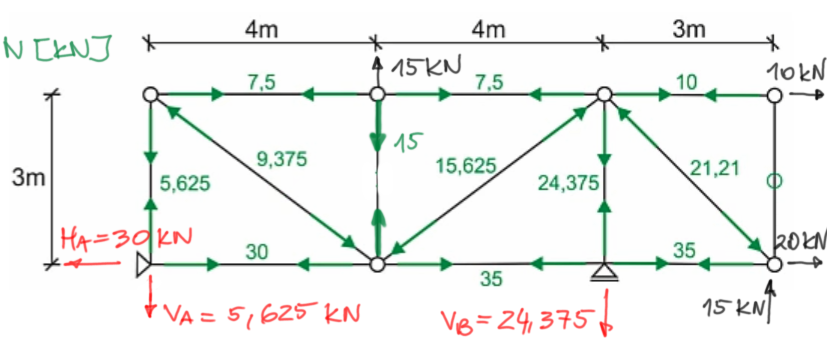
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.