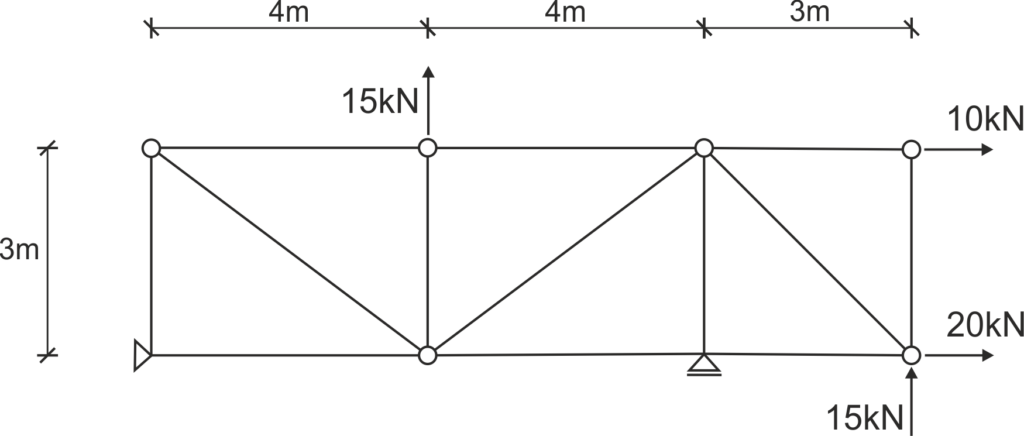
Solución
Para los curiosos, aquí está el enlace a la solución en Robot Structural Analysis:
kratownica1.rtd
Ejemplo de cálculo con comentarios
Contenido
Para una retícula dada, identifique las barras nulas y determine las fuerzas en todas las barras utilizando el método de Ritter.
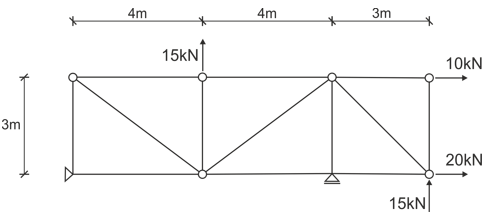
Solución
Paso 1
Enumerar las barras, marcar los nodos si es necesario y marcar las reacciones de soporte.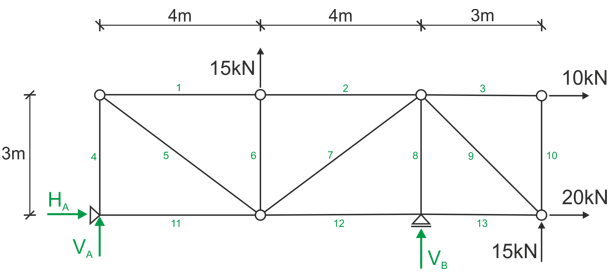
Paso 2
Escribir las ecuaciones de equilibrio estático y calcular las reacciones en los apoyos.
Paso 3
Realizar los cortes de Ritter.En principio, podemos hacerlo de cualquier manera, siempre que no cortemos más de 3 barras, ya que solo podemos calcular tres incógnitas en un solo corte.
Comencemos cortando las barras 2, 7 y 12 y hagamos una vista desde el lado izquierdo.

Guardaremos las ecuaciones de equilibrio estático.
Los llamados puntos de Ritter son los puntos de intersección de las direcciones de dos incógnitas.En la imagen de arriba, las fuerzas N2 y N7 se cruzan en el punto (1) y las fuerzas N7 y N12 se cruzan en el punto (2): estos son precisamente los puntos de Ritter. Normalmente, escribimos las sumas de momentos en los puntos de Ritter, a veces hay más de dos puntos si las fuerzas están en ángulos diferentes, entonces podemos escribir tres ecuaciones en forma de suma de momentos.
Si solo tenemos dos puntos de Ritter como aquí, no importa, escribimos dos sumas de momentos y como tercer ecuación podemos escribir la suma de proyecciones en el eje "x" o (mejor) en el eje "y", ya que solo la incógnita N7 entra en esta ecuación.
También podemos escribir la suma de momentos en otro punto para calcular la última incógnita, aquí se determinó el punto (3).
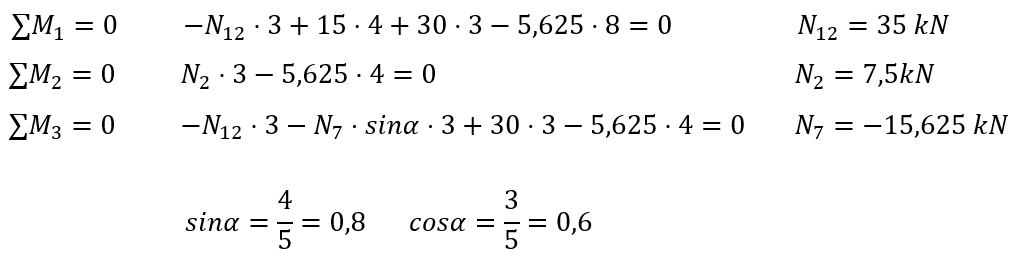
De manera análoga, realizamos el corte de Ritter a través de las barras 1, 5 y 11.
Vista desde el lado izquierdo.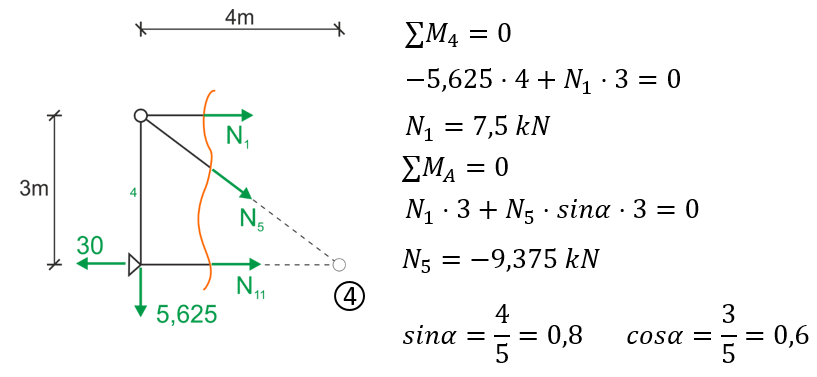
Finalmente, el corte de Ritter final a través de las barras 3, 9 y 13.
Vista desde el lado derecho.
Paso 5
Finalización de la solución del problema.Dibujemos el gráfico de las fuerzas normales en las barras que ya hemos calculado.
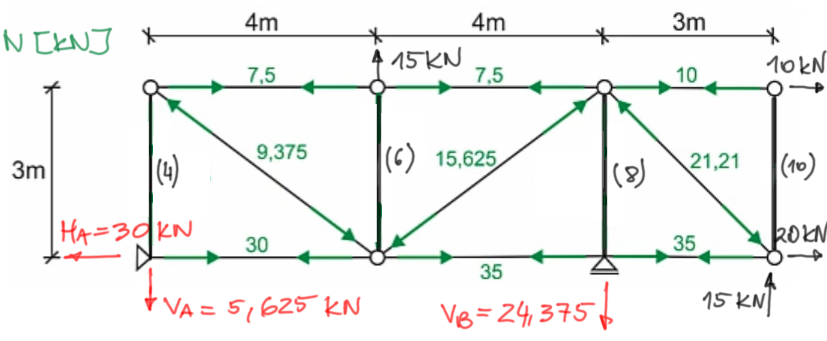 Gráfico de fuerzas normales, notación:
Gráfico de fuerzas normales, notación:
Hemos calculado las fuerzas en la mayoría de las barras (9 de 13). Nos quedan 4 barras (4, 6, 8 y 10) y tenemos tres opciones:
- Hacer más cortes. Ahora necesitaríamos cuatro cortes separados para calcular estas fuerzas, lo cual es un poco innecesario.
- Hacer el equilibrio de nodos en A,B, (3-10) y (1-2-6) y calcular las últimas cuatro fuerzas, definitivamente se dibuja menos al cortar un solo nodo que al hacer un corte más grande.
- Darse cuenta inteligentemente de que:
1) según el segundo teorema de las barras nulas, la barra (10) es nula,
2) se sigue del segundo teorema que básicamente
se deriva una regla adicional que, si la fuerza carga el nodo de tal manera que su dirección es colineal con una de las barras y ninguna otra fuerza se puede proyectar en esta línea, entonces la fuerza en la barra se transmite colinealmente.
Miremos la pasarela inferior y el nodo B: la fuerza de 35 kN en la barra horizontal se transmite de barra a barra como se ve en el gráfico,
mientras que la reacción VB=24,375 kN coloca una carga colineal en la barra (8) - por lo tanto, transmite directamente la fuerza tensil (porque vemos que la reacción VB actúa sobre la barra (8) y la somete a tracción).
finalmente, a partir de esto conocemos la fuerza en la barra (8)
3) siguiendo la misma regla, N6=15 kN
4) siguiendo la misma regla, N4=5,625 kN
Paso 5
Dibujemos el gráfico final de las fuerzas normales.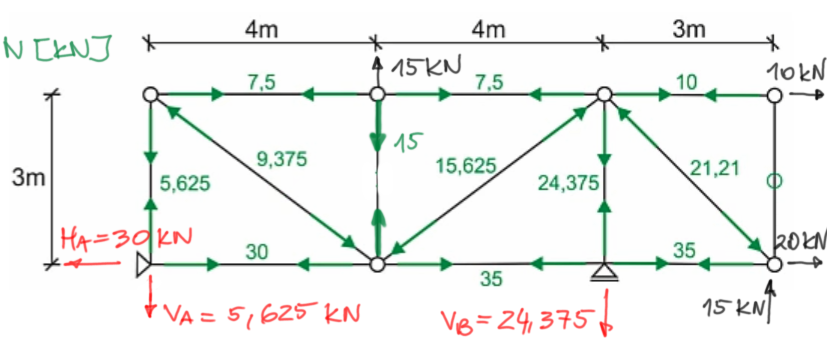
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.