Solution
Version YT
Classic version
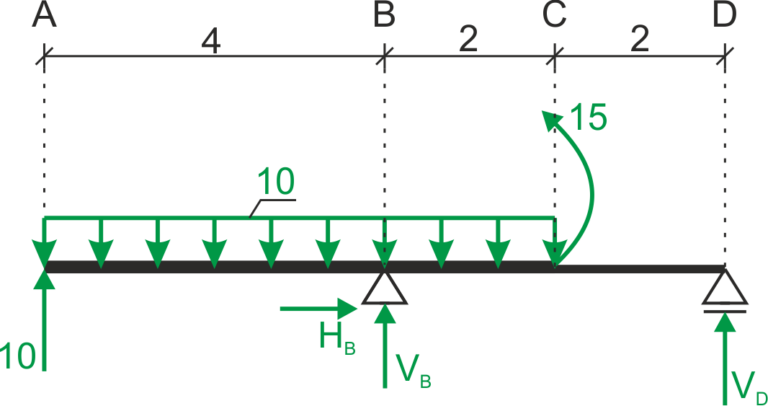
1. Marking characteristic points and reactions at supports
 \begin{aligned}
&\sum M_{D}=0 \\
&10 \cdot 8-60 \cdot 5-15+4 V_{B}=0 \\
&V_{B}=58.75 \mathrm{kN} \\
&\sum M_{B}=0 \\
&10 \cdot 4-60 \cdot 1-15-4 V_{D}=0 \\
&V_{D}=-8.75 \mathrm{kN} \\
&\sum Y=0 \\
&V_{B}+V_{D}-60+10=0 \\
&L=P
\end{aligned}
\begin{aligned}
&\sum M_{D}=0 \\
&10 \cdot 8-60 \cdot 5-15+4 V_{B}=0 \\
&V_{B}=58.75 \mathrm{kN} \\
&\sum M_{B}=0 \\
&10 \cdot 4-60 \cdot 1-15-4 V_{D}=0 \\
&V_{D}=-8.75 \mathrm{kN} \\
&\sum Y=0 \\
&V_{B}+V_{D}-60+10=0 \\
&L=P
\end{aligned}
3. Expressing internal force equations in individual segments of variability:
a) Segment AB 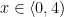
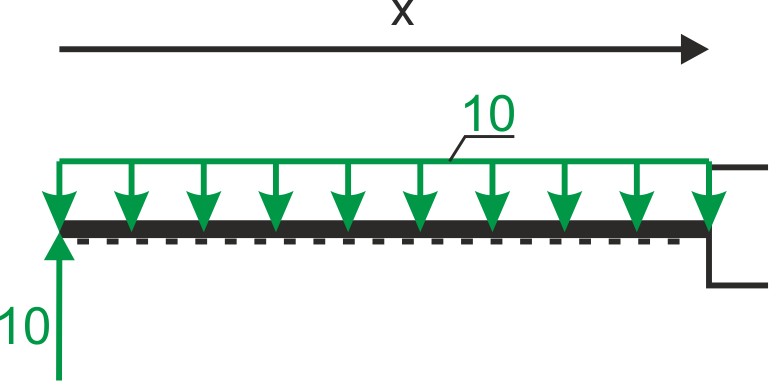 \begin{aligned}
&Q_{A B}=10-10 \cdot x \\
&Q_{A(0)}=10 \\
&Q_{B(4)}=-30 \\
&M_{A B}=10 \cdot x-10 \cdot \frac{x^{2}}{2} \\
&M_{A(0)}=0 \\
&M_{B(4)}=-40
\end{aligned}
\begin{aligned}
&Q_{A B}=10-10 \cdot x \\
&Q_{A(0)}=10 \\
&Q_{B(4)}=-30 \\
&M_{A B}=10 \cdot x-10 \cdot \frac{x^{2}}{2} \\
&M_{A(0)}=0 \\
&M_{B(4)}=-40
\end{aligned}
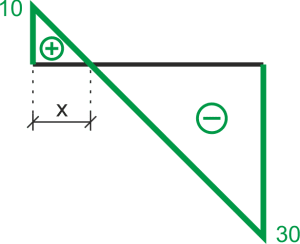 \begin{aligned} \\ &Q_{AB}=10-10\cdot x=0\\ &10=10x\\ &x=1m\\ \\ \end{aligned}
\begin{aligned} \\ &Q_{AB}=10-10\cdot x=0\\ &10=10x\\ &x=1m\\ \\ \end{aligned}
Extreme
\begin{aligned} \\ &\frac{10}{x}=\frac{30}{4-x} \ \Rightarrow \ x=1\\ &M_{max}=10\cdot 1 – 10\cdot(\frac{1}{2})^{2}=5\\ \\ \end{aligned}b) Segment BC 
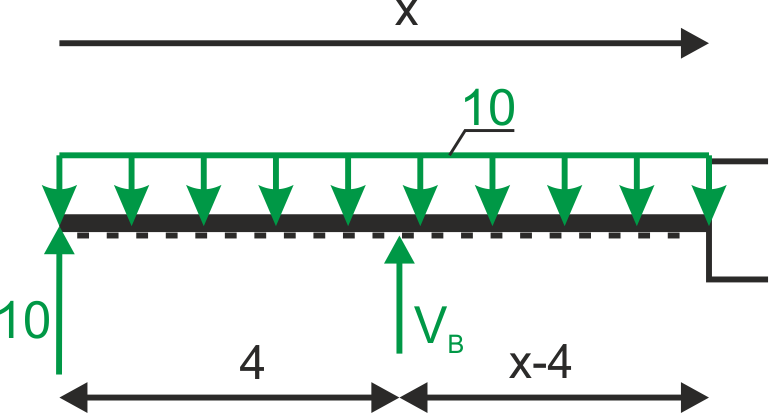
c) Segment DC 
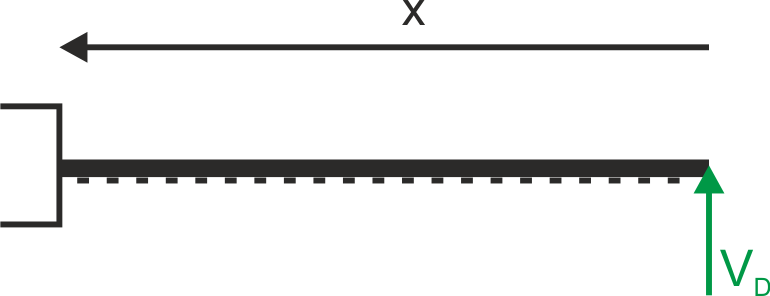
4. Final charts
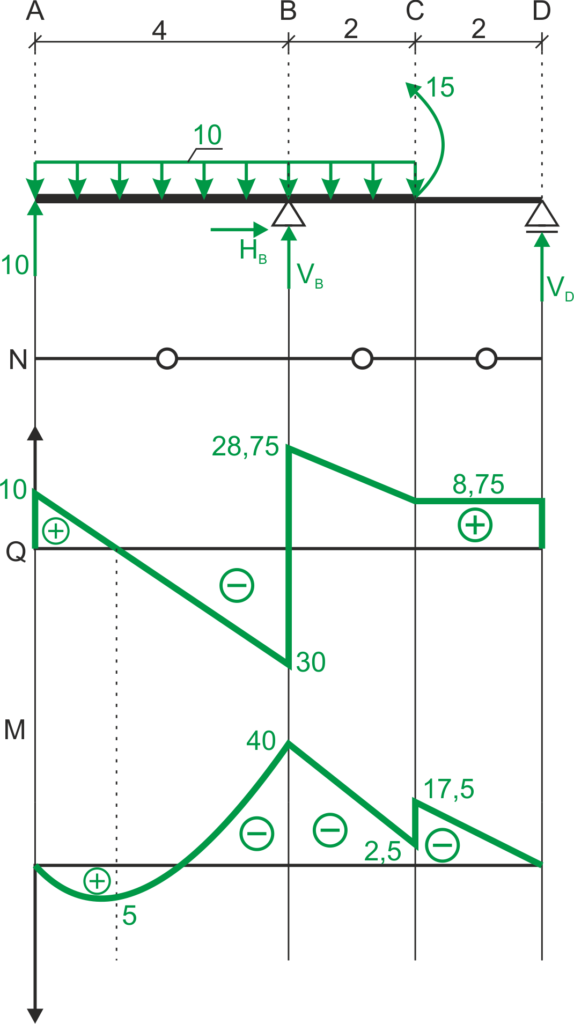
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.
