Solution
Version YT
Version classique
Détermination des réactions d'appui
Nous divisons la poutre en quatre poutres simples en remplaçant les articulations par des forces fictives.
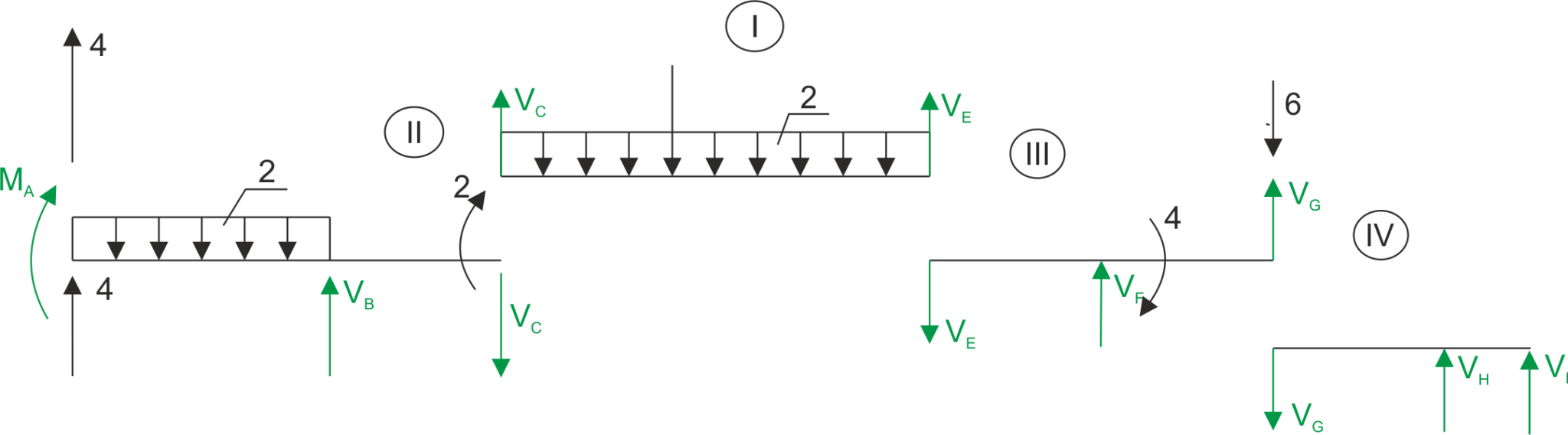
I
\begin{aligned} &\sum{M_C}=0 & 2\cdot 2+2\cdot 5\cdot 2,5-5V_{E}=0 && V_{E}=5,8\ kN\\ &\sum{M_E}=0 & V_{C}\cdot 5-2 \cdot 3-2\cdot 5 \cdot 2,5=0 && V_{C}=6,2\ kN\\ &\sum{y=0} & V_{C}+V_{E}-2-5\cdot 2=0 && L=P\\ \end{aligned}II
\begin{aligned} &\sum{y}=0 & V_{B}-V_{C}-2\cdot 3+4=0 && V_{B}=8,2\ kN\\ &\sum{M_B}=0 & M_{A}-2\cdot 3\cdot 1,5+2+V_{C}+4\cdot 3=0 && M_{A}=-17,4\ kN\\ \end{aligned}III
\begin{aligned} &\sum{M_F}=0 & 4+6\cdot 2-V_{G}\cdot 2-V_{E}\cdot 2=0 && V_{G}=2,2\ kN \\ &\sum{M_G}=0 & 4+V_{F}\cdot 2-4\cdot V_{E}=0 && V_{F}=9,6\ kN\\ &\sum{y}=0 & -V_{E}+V_{F}+V_{G}-6=0 && L=P\\ \end{aligned}IV
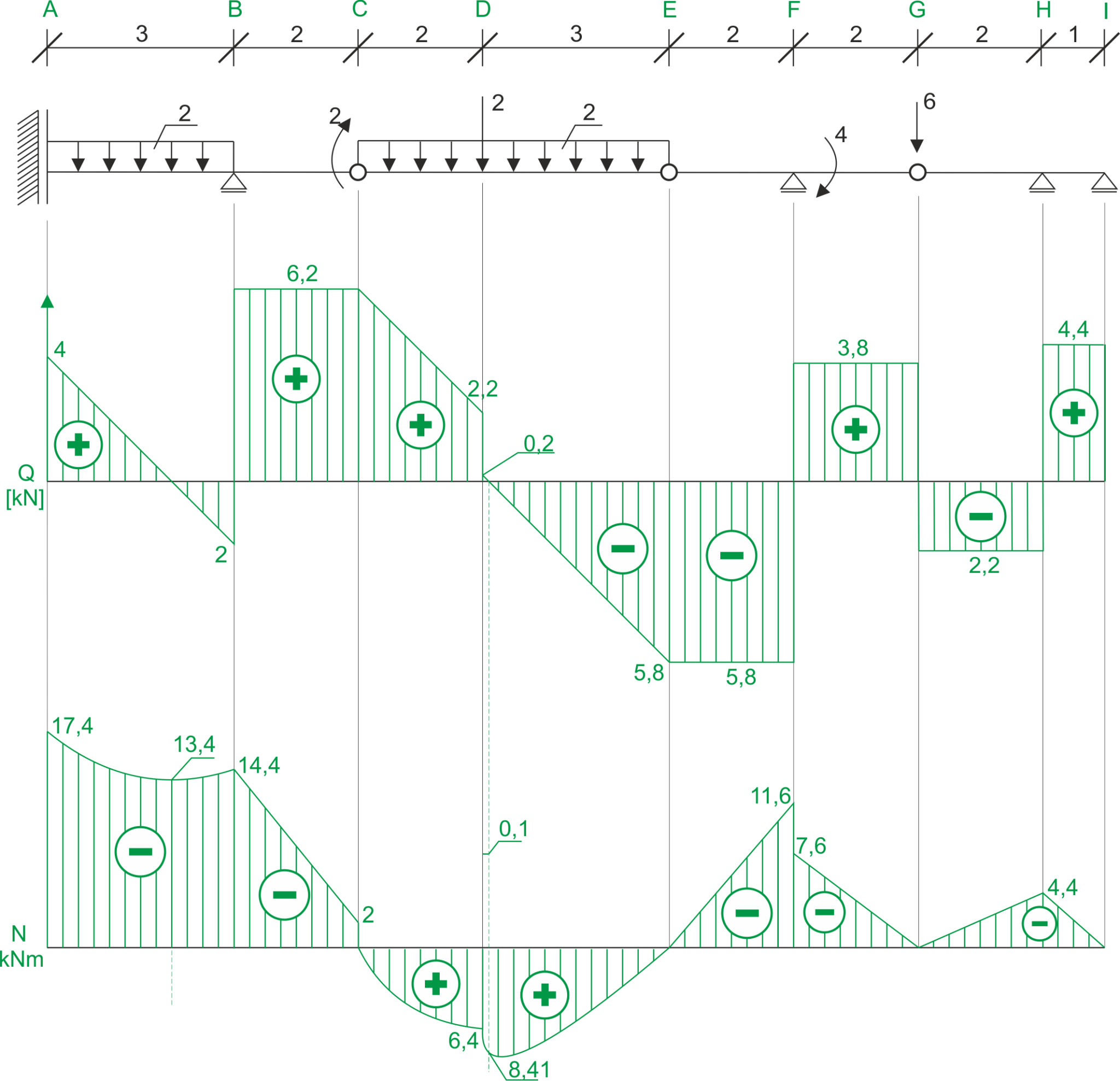
\begin{aligned} &\sum{M_M}=0 & -V_{G}\cdot 2-V_{I}\cdot 1=0 && V_{I}=-4,4\ kN\\ &\sum{M_I}=0 & V_{H}\cdot1-V_{G}\cdot 3=0 && V_{H}=6,6\ kN\\ &\sum{y}=0 & -V_{G}+V_{H}+V_{I}=0 && L=P\\ \end{aligned} \begin{aligned} &\frac{0,2}{x}=\frac{5,8}{3-x} &x=0,1 \end{aligned}Graphique
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.
