Solution
Classic version
Determination of support reactions
We divide the beam into four simple beams, replacing the hinges with fictitious forces.
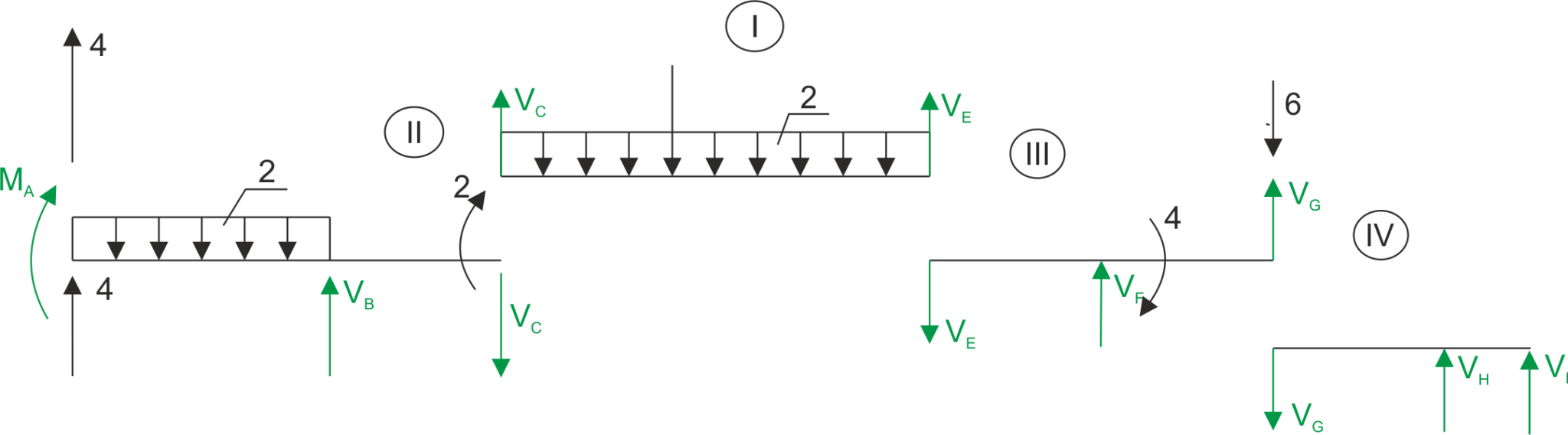
I
\begin{aligned} &\sum{M_C}=0 & 2\cdot 2+2\cdot 5\cdot 2.5-5V_{E}=0 && V_{E}=5.8\ kN\\ &\sum{M_E}=0 & V_{C}\cdot 5-2 \cdot 3-2\cdot 5 \cdot 2.5=0 && V_{C}=6.2\ kN\\ &\sum{y}=0 & V_{C}+V_{E}-2-5\cdot 2=0 && L=P\\ \end{aligned}II
\begin{aligned} &\sum{y}=0 & V_{B}-V_{C}-2\cdot 3+4=0 && V_{B}=8.2\ kN\\ &\sum{M_B}=0 & M_{A}-2\cdot 3\cdot 1.5+2+V_{C}+4\cdot 3=0 && M_{A}=-17.4\ kN\\ \end{aligned}III
\begin{aligned} &\sum{M_F}=0 & 4+6\cdot 2-V_{G}\cdot 2-V_{E}\cdot 2=0 && V_{G}=2.2\ kN \\ &\sum{M_G}=0 & 4+V_{F}\cdot 2-4\cdot V_{E}=0 && V_{F}=9.6\ kN\\ &\sum{y}=0 & -V_{E}+V_{F}+V_{G}-6=0 && L=P\\ \end{aligned}IV
\begin{aligned} &\sum{M_M}=0 & -V_{G}\cdot 2-V_{I}\cdot 1=0 && V_{I}=-4.4\ kN\\ &\sum{M_I}=0 & V_{H}\cdot1-V_{G}\cdot 3=0 && V_{H}=6.6\ kN\\ &\sum{y}=0 & -V_{G}+V_{H}+V_{I}=0 && L=P\\ \end{aligned} \begin{aligned} &\frac{0.2}{x}=\frac{5.8}{3-x} &x=0.1 \end{aligned}Chart
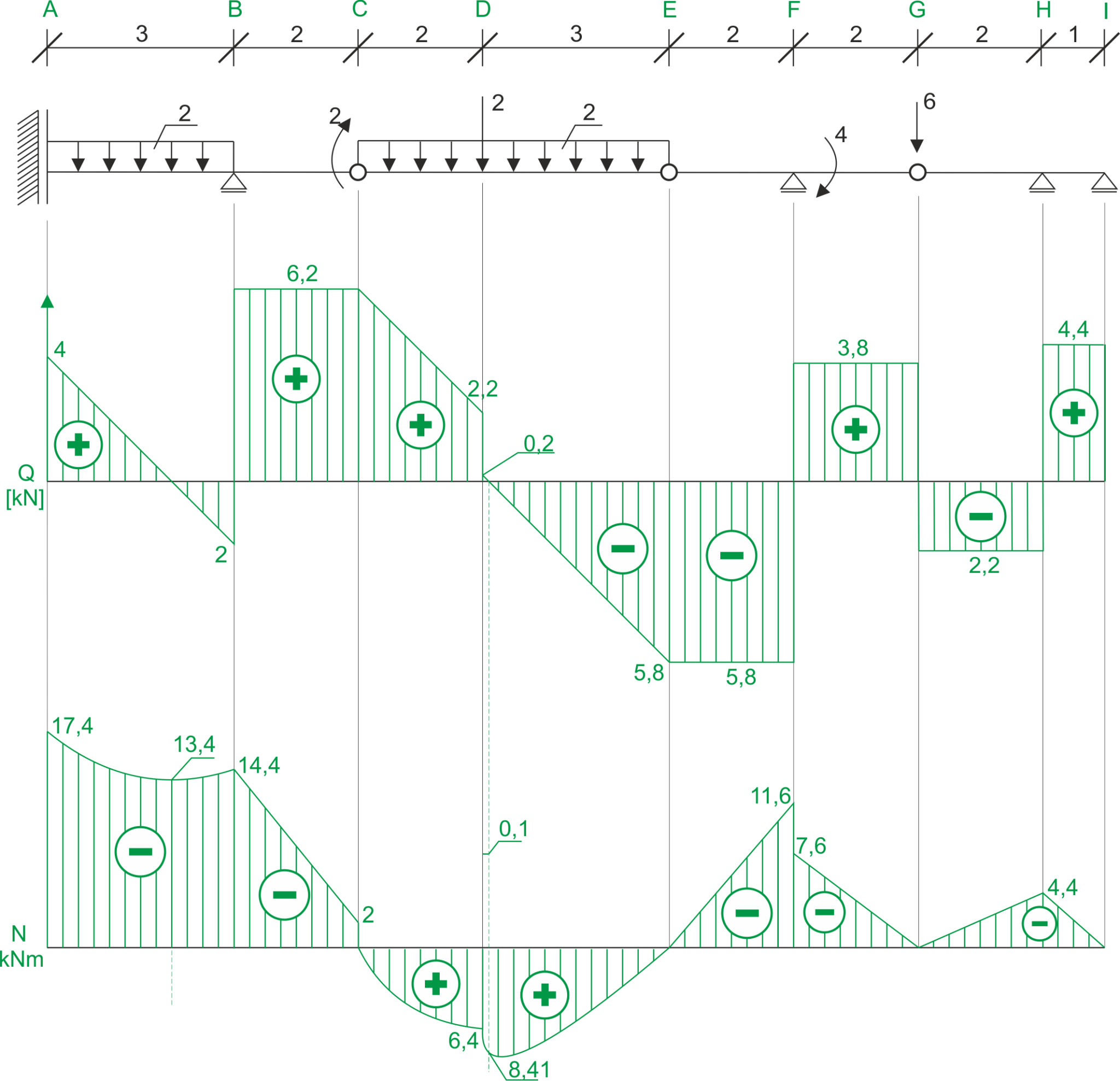
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.
