Nous vous encourageons à regarder la solution de cet exemple (comme les autres) sur notre chaîne YouTube. J'explique étape par étape comment résoudre cet exercice. Regarder cette vidéo vous aidera également à comprendre les autres exemples sur notre site.

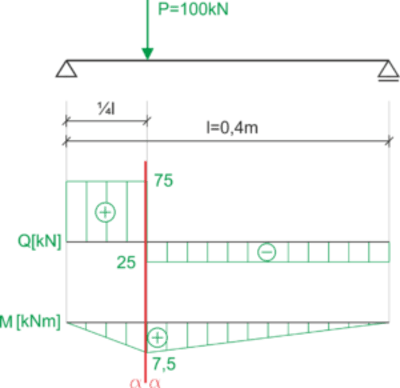\begin{aligned} &z_1=50\ mm &A_1=2000\ mm^2\\ &z_2=110\ mm &A_2=2000\ mm^2\\ &z_c=\frac{z_1\cdot A_1+z_2\cdot A_2}{A_1+A_2} &z_c=80\ mm\\ &I_{yc}=\frac{20\cdot 100^3}{12}+2000\cdot (50 80)^2+\frac{100\cdot 20^3}{12}+2000\cdot (110 80)^2\\ &I_{zc}=5333333\ cm^4=5,33\cdot 10^{6}\ m^4\\ \end{aligned}

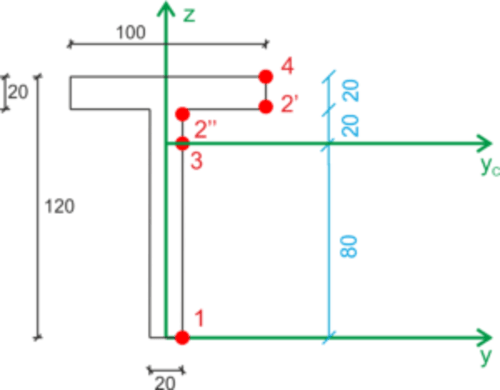
Contraintes normales

\begin{aligned} &\sigma=\frac{M}{Iy}\cdot z \\ &\sigma=\frac{-7,5\cdot 10^3}{5,33\cdot 10^{-6}}\cdot z=-1,407\cdot 10^9\cdot z\\ &\sigma_1=112,56\ MPa\\ &\sigma_3=0\ MPa\\ &\sigma_2=-28,14\ MPa\\ &\sigma_4=-56,28\ MPa\\ \end{aligned}

Contraintes tangentes

\begin{aligned} &\tau=\frac{T⋅S}{Iy⋅b}\\ &\tau=\frac{75\cdot 10^3}{5,33\cdot 10^{-6}}\cdot \frac{S}{b}=1,407\cdot 10^{10}\cdot \frac{S}{b}\\ \\ \\ \\ &L'inertie statique\\ &S_1=S_4=0\\ &S_3=100⋅20⋅30+20⋅20⋅10=64000\ cm^3=64⋅10^{-6}\ m^3\\ &S_2=100⋅20⋅30=60000\ cm^3=60⋅10^{-6}\ m^3\\ \\ &\tau_3=1,407⋅10^9⋅\frac{64⋅10^{-6}}{0,02}=45,03\ MPa\\ &\tau_2 bis=1,407⋅10^{10}⋅\frac{60⋅10^{-6}}{0,02}=42,21\ MPa\\ &\tau_2 prim=8,44\ MPa\\ \end{aligned}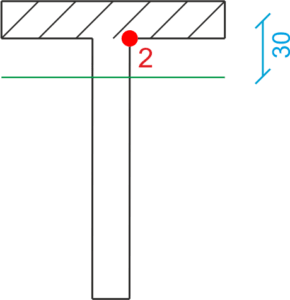

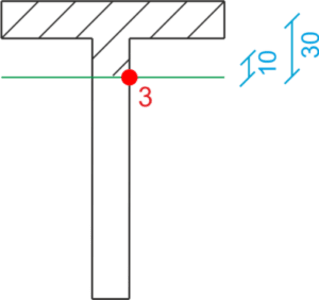
Valeurs des contraintes aux points critiques de la section dangereuse.

\begin{aligned} &\sigma_{red}^{HMH}=\sqrt{\sigma^2+3⋅\tau^2}\\ &\sigma_{red}^{HMH}(2)=\sqrt{28,14^2+3⋅42,21^2}=78,34\ MPa\\ &\sigma_{red}^{HMH}(3)=\sqrt{0^2+3⋅45,03^2}=78\ MPa\\ &\sigma_{red}^{HMH}(1)=\sqrt{112,56^2+3⋅0^2}=112,56\ MPa\\ \end{aligned}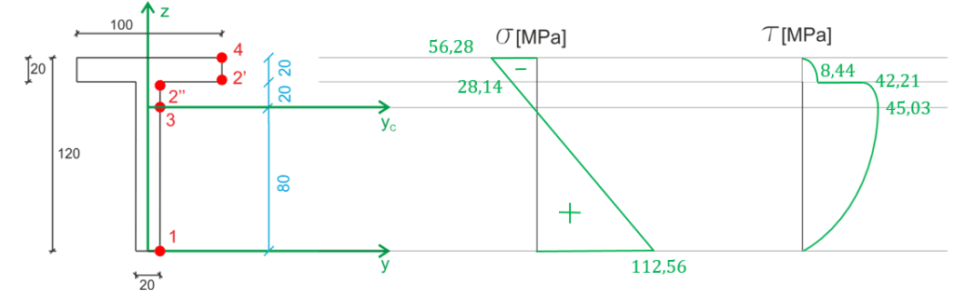

Source:

Stanisław Wolny, Adam Siemieniec, Wytrzymałość materialów część 1, Wydawnictwo AGH, Kraków 2002, Przykład 9.38 s. 382