Solution
We encourage you to watch the solution to this example (as well as the others) on our YouTube channel. In the video, I explain step by step how to solve this problem. Watching this video will also help you understand the other examples on our website.
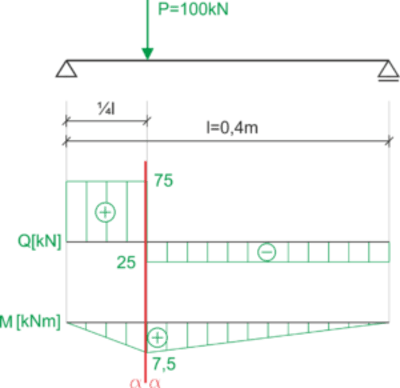 \begin{aligned} &z_1=50\ mm &A_1=2000\ mm^2\\ &z_2=110\ mm &A_2=2000\ mm^2\\ &z_c=\frac{z_1\cdot A_1+z_2\cdot A_2}{A_1+A_2} &z_c=80\ mm\\ &I_{yc}=\frac{20\cdot 100^3}{12}+2000\cdot (50 80)^2+\frac{100\cdot 20^3}{12}+2000\cdot (110 80)^2\\ &I_{zc}=5333333\ cm^4=5.33\cdot 10^{6}\ m^4\\ \end{aligned}
\begin{aligned} &z_1=50\ mm &A_1=2000\ mm^2\\ &z_2=110\ mm &A_2=2000\ mm^2\\ &z_c=\frac{z_1\cdot A_1+z_2\cdot A_2}{A_1+A_2} &z_c=80\ mm\\ &I_{yc}=\frac{20\cdot 100^3}{12}+2000\cdot (50 80)^2+\frac{100\cdot 20^3}{12}+2000\cdot (110 80)^2\\ &I_{zc}=5333333\ cm^4=5.33\cdot 10^{6}\ m^4\\ \end{aligned}
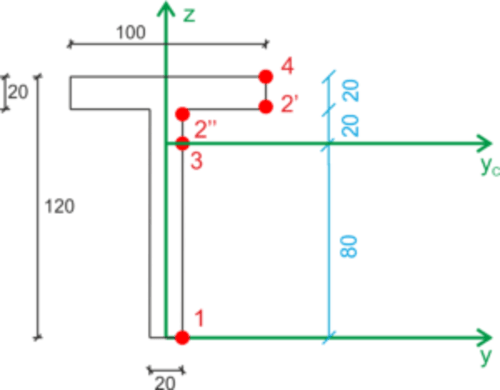
Normal stresses
\begin{aligned} &\sigma=\frac{M}{Iy}\cdot z \\ &\sigma=\frac{-7.5\cdot 10^3}{5.33\cdot 10^{-6}}\cdot z=-1.407\cdot 10^9\cdot z\\ &\sigma_1=112.56\ MPa\\ &\sigma_3=0\ MPa\\ &\sigma_2=-28.14\ MPa\\ &\sigma_4=-56.28\ MPa\\ \end{aligned}Shear stresses
\begin{aligned} &\tau=\frac{T⋅S}{Iy⋅b}\\ &\tau=\frac{75\cdot 10^3}{5.33\cdot 10^{-6}}\cdot \frac{S}{b}=1.407\cdot 10^{10}\cdot \frac{S}{b}\\ \\ \\ \\ &Moment of inertia\\ &S_1=S_4=0\\ &S_3=100⋅20⋅30+20⋅20⋅10=64000\ cm^3=64\cdot 10^{-6}\ m^3\\ &S_2=100⋅20⋅30=60000\ cm^3=60\cdot 10^{-6}\ m^3\\ \\ &\tau_3=1.407⋅10^9⋅\frac{64\cdot 10^{-6}}{0.02}=45.03\ MPa\\ &\tau_2 bis=1.407⋅10^{10}⋅\frac{60\cdot 10^{-6}}{0.02}=42.21\ MPa\\ &\tau_2 prim=8.44\ MPa\\ \end{aligned}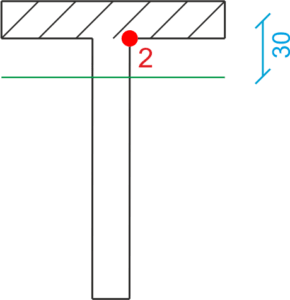
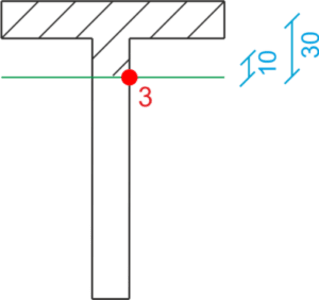
Stress values at critical points of the dangerous section.
\begin{aligned} &\sigma_{red}^{HMH}=\sqrt{\sigma^2+3⋅\tau^2}\\ &\sigma_{red}^{HMH}(2)=\sqrt{28.14^2+3⋅42.21^2}=78.34\ MPa\\ &\sigma_{red}^{HMH}(3)=\sqrt{0^2+3⋅45.03^2}=78\ MPa\\ &\sigma_{red}^{HMH}(1)=\sqrt{112.56^2+3⋅0^2}=112.56\ MPa\\ \end{aligned}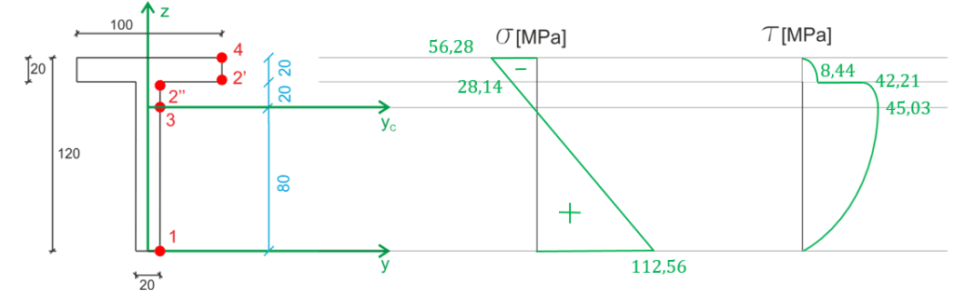
Source:
Stanisław Wolny, Adam Siemieniec, Strength of Materials Part 1, AGH University of Science and Technology Press, Krakow 2002, Example 9.38 p. 382
