Solution
Nous vous encourageons à regarder la solution de cet exemple (ainsi que des autres) sur notre chaîne YouTube. J'explique étape par étape comment résoudre cet exercice. Regarder cette vidéo vous aidera également à comprendre les autres exemples sur notre site.
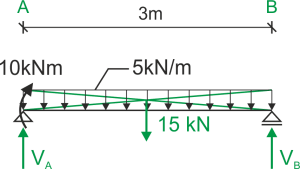
Réactions
 \begin{aligned}\\
&\sum{M_A}=0\\
&10+5\cdot 3\cdot \frac{3}{2}-3\cdot V_B=0 & V_B=10,83\ kN\\
&\sum{M_B}=0\\
&10+3\cdot V_A-3\cdot 5\cdot \frac{3}{2}=0 & V_A=4,17\ kN\\
&\sum{Y}=0 & V_A+V_C-5\cdot 3=0\\
\end{aligned}
\begin{aligned}\\
&\sum{M_A}=0\\
&10+5\cdot 3\cdot \frac{3}{2}-3\cdot V_B=0 & V_B=10,83\ kN\\
&\sum{M_B}=0\\
&10+3\cdot V_A-3\cdot 5\cdot \frac{3}{2}=0 & V_A=4,17\ kN\\
&\sum{Y}=0 & V_A+V_C-5\cdot 3=0\\
\end{aligned}
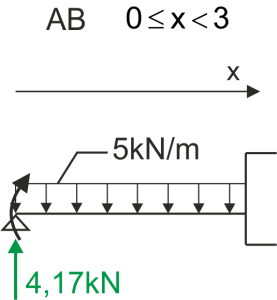 \begin{aligned}\\
&Q_{AB}=4,17-5x & Q_{AB}=0\\
&Q_A(0)=4,17\ kN & x=0,834\ m\\
&Q_B(3)=-10,83\ kN\\
&M_{AB}=10+4,17x-5x\cdot \frac{x}{2}\\
&M_A(0)=10\ kNm & M_B(3)=0\ kNm\\
&M_{max}(0,834)=11,739\approx 11,74\ kNm
\end{aligned}
\begin{aligned}\\
&Q_{AB}=4,17-5x & Q_{AB}=0\\
&Q_A(0)=4,17\ kN & x=0,834\ m\\
&Q_B(3)=-10,83\ kN\\
&M_{AB}=10+4,17x-5x\cdot \frac{x}{2}\\
&M_A(0)=10\ kNm & M_B(3)=0\ kNm\\
&M_{max}(0,834)=11,739\approx 11,74\ kNm
\end{aligned}
Diagrammes des efforts tranchants et des moments fléchissants
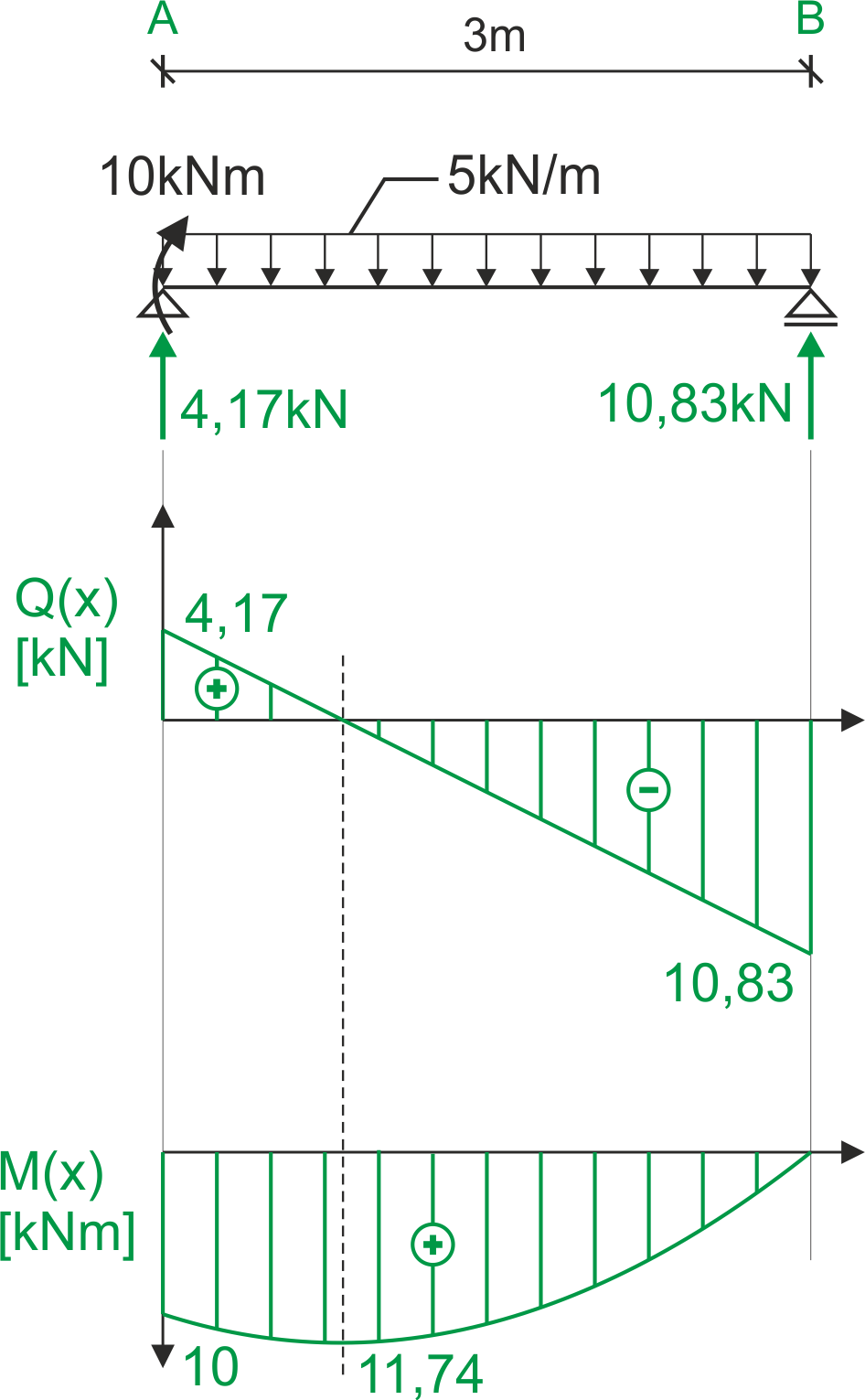
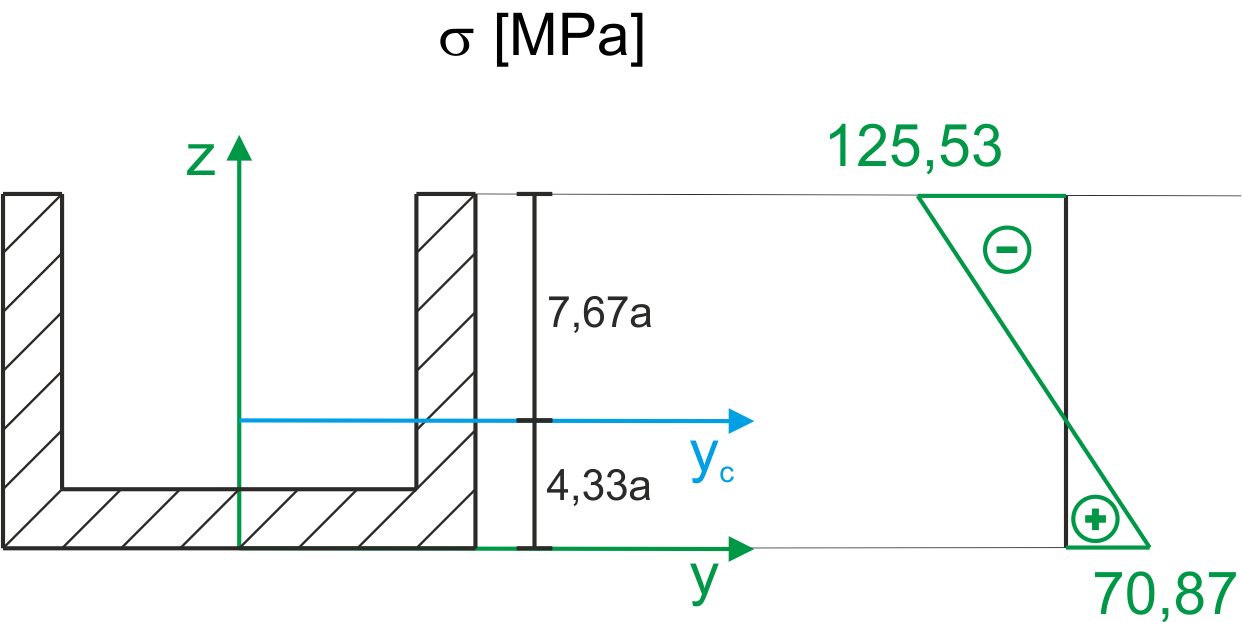
Dimensionnement
\begin{aligned}\\ &k_r=120\ MPa & k_c=160\ MPa\\ &z_1=6a & A_1=12a\cdot 16a=192a^2\\ &z_2=a & A_2=10a\cdot 12a=120a^2\\ &z_c=\frac{z_1\cdot A_1-z_2\cdot A_2}{A_1-A_2}=4,33a\\ &I_{y_c}=\frac{16\cdot 12^3}{12}+192(6-4,33)^2-[\frac{12\cdot 10^3}{12}+120(7-4,33)^2]=984a^4\\ \end{aligned}La distance par rapport au centre de gravité aux fibres supérieures est plus grande, donc les contraintes sur les fibres supérieures seront plus grandes. Les fibres supérieures sont comprimées et les inférieures sont étirées. Des contraintes plus élevées (de compression) sur les fibres supérieures rencontrent une résistance plus élevée à la compression, et des contraintes (moins élevées) de traction rencontrent une résistance plus faible à la traction. Par conséquent, il est impossible de déterminer clairement quelle condition sera décisive, il est donc nécessaire de vérifier les deux conditions.
\begin{aligned}\\ &W_g=\frac{I_{y_c}}{z_g}=\frac{984a^4}{7,67a}=128,29a^3\\ &W_d=\frac{I_{y_c}}{z_d}=\frac{984a^4}{4,33a}=227,25a^3\\ \\ &\frac{M_{max}}{W_g}\le k_c \Rightarrow \frac{11,74\cdot 10^3}{128,29a^3}\le 160\cdot 10^6\\ &a\ge 8,3\ mm\\ &\frac{M_{max}}{W_d}\le k_r \Rightarrow \frac{11,74\cdot 10^3}{227,25a^3}\le 120\cdot 10^6\\ &a\ge 7,55\ mm\\ \\ &a=9\ mm\\ &\sigma_g=\frac{11,74\cdot 10^3}{128,29\cdot (9\cdot 10^{-3})^3}=125,53\ MPa\\ &\sigma_d=\frac{11,74\cdot 10^3}{227,25\cdot (9\cdot 10^{-3})^3}=70,866\ MPa\\ \end{aligned}Diagramme des contraintes