Solución
Te animamos a ver la solución de este ejemplo (y otros) en nuestro canal de YouTube. Explico paso a paso cómo resolver este problema. Ver este video también te ayudará a entender otros ejemplos en nuestro sitio.
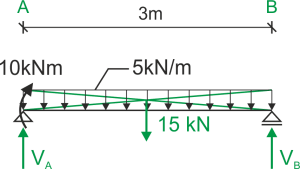
Reacciones
 \begin{aligned}\\
&\sum{M_A}=0\\
&10+5\cdot 3\cdot \frac{3}{2}-3\cdot V_B=0 & V_B=10,83\ kN\\
&\sum{M_B}=0\\
&10+3\cdot V_A-3\cdot 5\cdot \frac{3}{2}=0 & V_A=4,17\ kN\\
&\sum{Y}=0 & V_A+V_C-5\cdot 3=0\\
\end{aligned}
\begin{aligned}\\
&\sum{M_A}=0\\
&10+5\cdot 3\cdot \frac{3}{2}-3\cdot V_B=0 & V_B=10,83\ kN\\
&\sum{M_B}=0\\
&10+3\cdot V_A-3\cdot 5\cdot \frac{3}{2}=0 & V_A=4,17\ kN\\
&\sum{Y}=0 & V_A+V_C-5\cdot 3=0\\
\end{aligned}
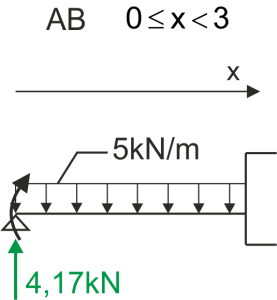 \begin{aligned}\\
&Q_{AB}=4,17-5x & Q_{AB}=0\\
&Q_A(0)=4,17\ kN & x=0,834\ m\\
&Q_B(3)=-10,83\ kN\\
&M_{AB}=10+4,17x-5x\cdot \frac{x}{2}\\
&M_A(0)=10\ kNm & M_B(3)=0\ kNm\\
&M_{max}(0,834)=11,739\approx 11,74\ kNm
\end{aligned}
\begin{aligned}\\
&Q_{AB}=4,17-5x & Q_{AB}=0\\
&Q_A(0)=4,17\ kN & x=0,834\ m\\
&Q_B(3)=-10,83\ kN\\
&M_{AB}=10+4,17x-5x\cdot \frac{x}{2}\\
&M_A(0)=10\ kNm & M_B(3)=0\ kNm\\
&M_{max}(0,834)=11,739\approx 11,74\ kNm
\end{aligned}
Gráfico de fuerzas cortantes y momentos de flexión
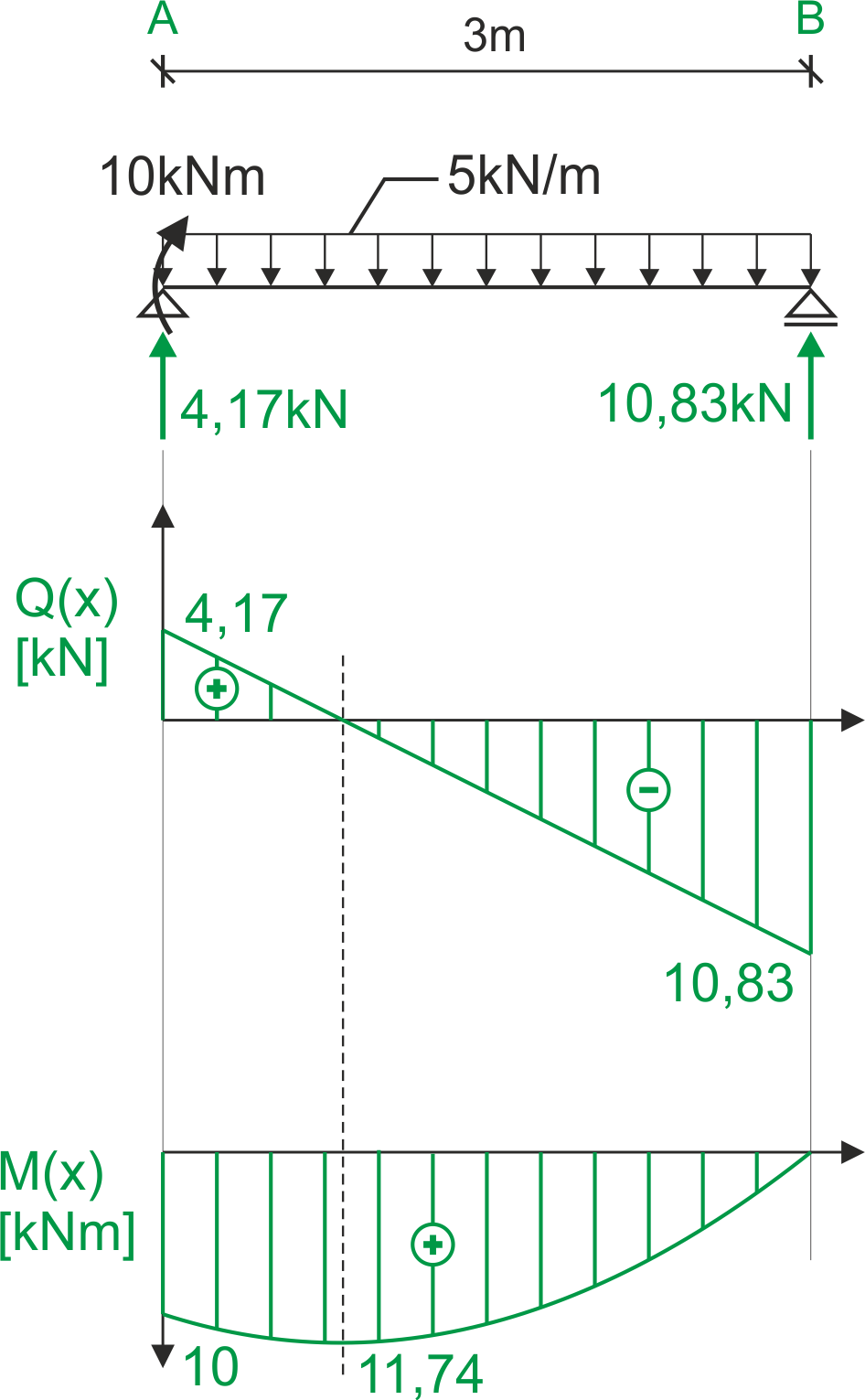
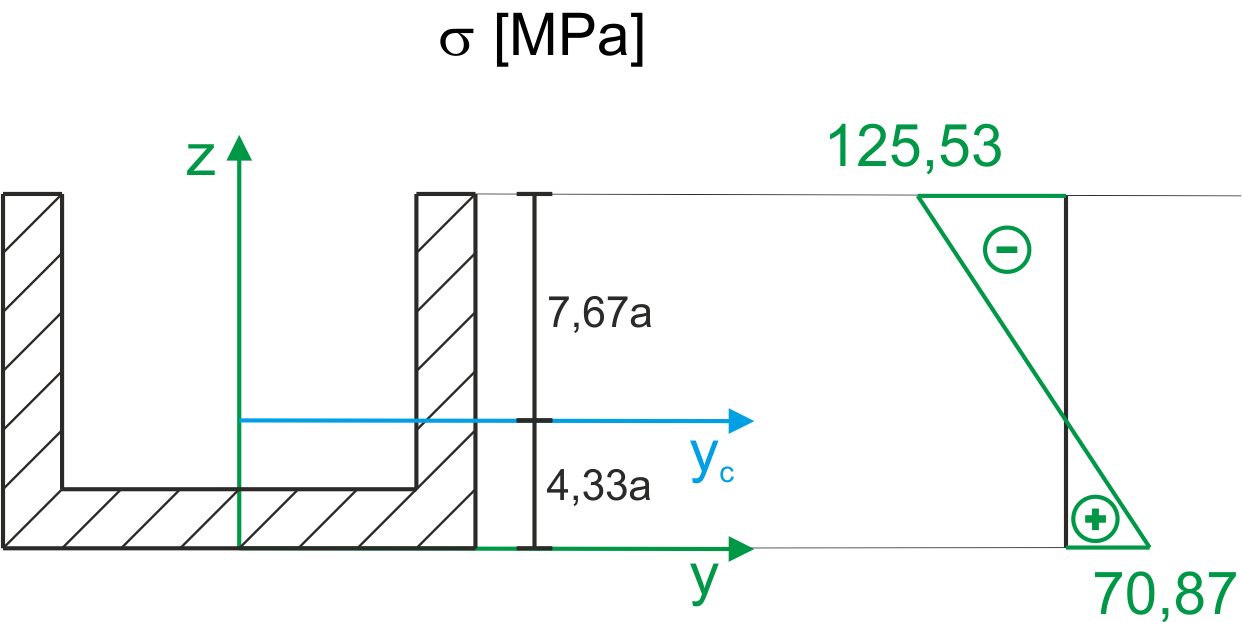
Dimensionamiento
\begin{aligned}\\ &k_r=120\ MPa & k_c=160\ MPa\\ &z_1=6a & A_1=12a\cdot 16a=192a^2\\ &z_2=a & A_2=10a\cdot 12a=120a^2\\ &z_c=\frac{z_1\cdot A_1-z_2\cdot A_2}{A_1-A_2}=4,33a\\ &I_{y_c}=\frac{16\cdot 12^3}{12}+192(6-4,33)^2-[\frac{12\cdot 10^3}{12}+120(7-4,33)^2]=984a^4\\ \end{aligned}La distancia desde el centro de gravedad hasta las fibras superiores es mayor, por lo que las tensiones en las fibras superiores serán mayores. Las fibras superiores se comprimen y las inferiores se tensionan. Las tensiones mayores (compresivas) en las fibras superiores se encuentran con una resistencia mayor a la compresión, y las tensiones (menores) de tracción se encuentran con una resistencia menor a la tracción. Por lo tanto, no podemos determinar de manera unívoca qué condición será la determinante, por lo que debemos verificar ambas condiciones.
\begin{aligned}\\ &W_g=\frac{I_{y_c}}{z_g}=\frac{984a^4}{7,67a}=128,29a^3\\ &W_d=\frac{I_{y_c}}{z_d}=\frac{984a^4}{4,33a}=227,25a^3\\ \\ &\frac{M_{max}}{W_g}\le k_c \Rightarrow \frac{11,74\cdot 10^3}{128,29a^3}\le 160\cdot 10^6\\ &a\ge 8,3\ mm\\ &\frac{M_{max}}{W_d}\le k_r \Rightarrow \frac{11,74\cdot 10^3}{227,25a^3}\le 120\cdot 10^6\\ &a\ge 7,55\ mm\\ \\ &a=9\ mm\\ &\sigma_g=\frac{11,74\cdot 10^3}{128,29\cdot (9\cdot 10^{-3})^3}=125,53\ MPa\\ &\sigma_d=\frac{11,74\cdot 10^3}{227,25\cdot (9\cdot 10^{-3})^3}=70,866\ MPa\\ \end{aligned}Gráfico de tensiones