Solution
Caractéristiques géométriques, moments d'inertie centraux
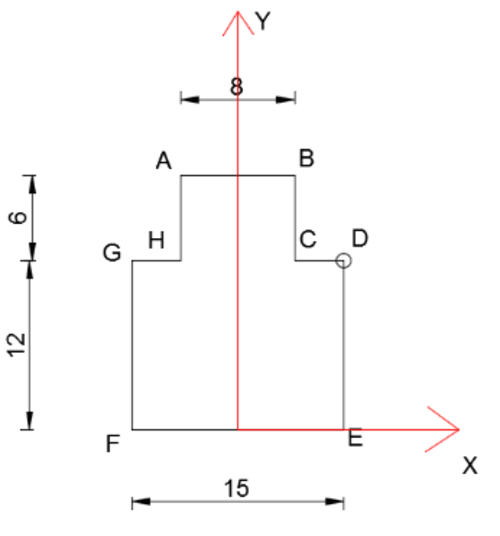
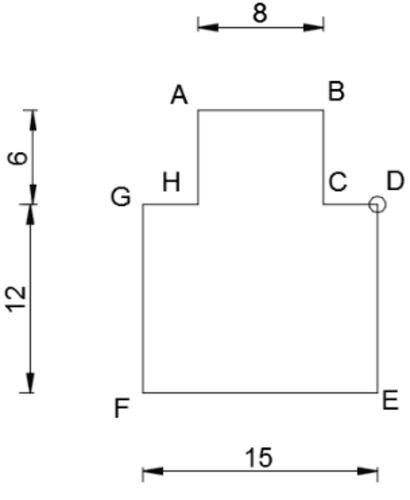
Figure 1 - grand rectangle, Figure 2 - petit rectangle
\begin{aligned} a&A_1 =180 cm^2\\ &A_2 =48 cm^2\\ &A=A_1 +A_2=228 cm^2\\ &y_1 =6 cm\\ &y_2 =15 cm\\ &y_c=\frac{y_1 ⋅A_1+ y_2 ⋅A_2}{A_1 +A_2}=7,89 cm\\ \end{aligned}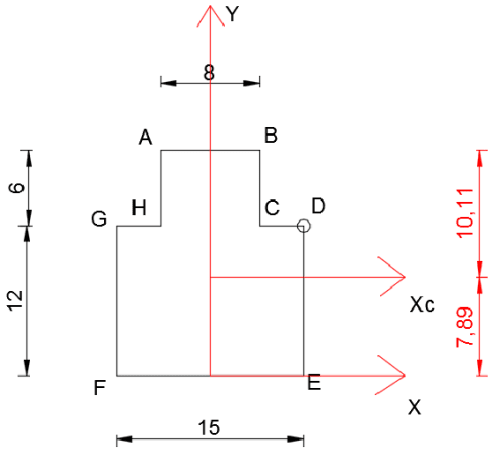 \begin{aligned} &I_{xc}=\frac{15\cdot 12^3}{12}+A_1\cdot (y_1-y_c)^2+\frac{8\cdot 6^3}{12}+A_2\cdot (y_2-y_c)^2=5373,47 cm^4\\ &I_{yc}=\frac{12\cdot 15^3}{12}+\frac{6\cdot 8^3}{12}=3631 cm^4\\ \end{aligned}
\begin{aligned} &I_{xc}=\frac{15\cdot 12^3}{12}+A_1\cdot (y_1-y_c)^2+\frac{8\cdot 6^3}{12}+A_2\cdot (y_2-y_c)^2=5373,47 cm^4\\ &I_{yc}=\frac{12\cdot 15^3}{12}+\frac{6\cdot 8^3}{12}=3631 cm^4\\ \end{aligned}
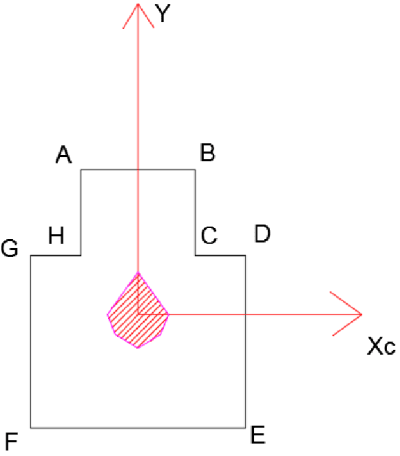
La force au point D dirigée "vers la feuille" (compression) crée des moments Mx et My dans les directions indiquées sur le schéma ci-dessous (règle de la main droite).
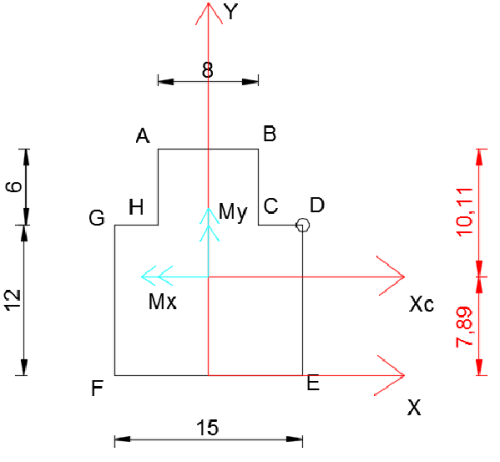
Détermination de l'équation de l'axe neutre
\begin{aligned} &N=-60 kN\\ &M_y=-|N|\cdot 0,075=-4,5 kNm\\ &M_x=-|N|\cdot |(0,12-0,0789)|=-2,466 kNm\\ &\sigma_x=\frac{-60\cdot 10^3}{228\cdot 10^{-4}}-\frac{2,466\cdot 10^3}{5373,37\cdot 10^{-8}}y-\frac{4,5\cdot 10^3}{3631\cdot 10^{-8}}x=0\\ &y=-2,7x-5,7\\ \end{aligned}Deux points quelconques définissent une droite (axe neutre).
\begin{aligned} &x=1, y=-8,4\\ &x=-1, y=-3\\ \end{aligned}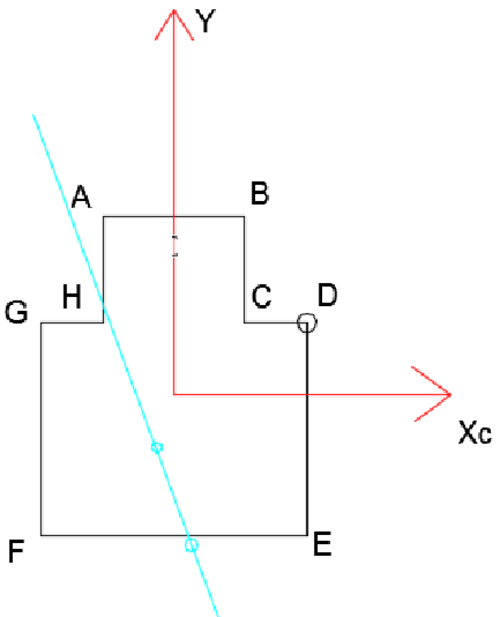
Contraintes aux points caractéristiques
\(\sigma=\frac{-60\cdot 10^3}{0.023}-\frac{2,466\cdot 10^3}{5373,37\cdot 10^{-8}}y-\frac{4,5\cdot 10^3}{3631\cdot 10^{-8}}x\)Point A (x=-4 cm, y=10,11 cm)
\(\sigma=-2,29 MPa\)Point B (x=4 cm, y=10,11 cm)
\(\sigma=-12,21 MPa\)Point C (x=4 cm, y=(12-7,89) cm)
\(\sigma=-9,45 MPa\)Point D (x=7,5 cm, y=(12-7,89) cm)
\(\sigma=-13,79 MPa\)Point E (x=7,5 cm, y=-7,89 cm)
\(\sigma=-8,28 MPa\)Point F (x=-7,5 cm, y=-7,89 cm)
\(\sigma=10,31 MPa\)Point G (x=-7,5 cm, y=(12-7,89) cm)
\(\sigma=4,8 MPa\)Point H (x=-4 cm, y=(12-7,89) cm)
\(\sigma=0,46 MPa\)Volume de contraintes
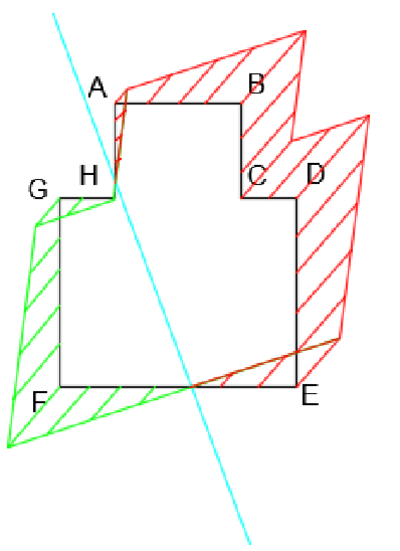
Noyau de la section
Nous marquons les tangentes à la section (violet), nous allons déterminer un point d'angle du noyau de la section pour chaque tangente.
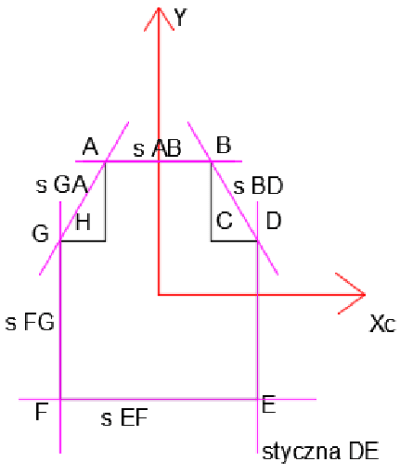 \begin{aligned} &i_x^2=\frac{I_{xc}}{A}=23,57 cm^2\\ &i_y^2=\frac{I_{yc}}{A}=15,93 cm^2\\ \end{aligned}
\begin{aligned} &i_x^2=\frac{I_{xc}}{A}=23,57 cm^2\\ &i_y^2=\frac{I_{yc}}{A}=15,93 cm^2\\ \end{aligned}
Nous utiliserons notamment l'équation de la droite passant par deux points :
\begin{aligned} &y-y_1=\frac{y_2-y_1}{x_2-x_1}\cdot (x-x_1)\\ \end{aligned}axe neutre D-E
\begin{aligned} &a_y=\infty\\ &a_x=7,5 cm\\ &y=-\frac{i_x}{a_y}=0 cm\\ &x=-\frac{i_y}{a_x}=-2,12 cm\\ \end{aligned}axe neutre E-F
\begin{aligned} &a_y=-7,89 cm\\ &a_x=\infty\\ &y=-\frac{i_x}{a_y}=2,99 cm\\ &x=-\frac{i_y}{a_x}=0 cm\\ \end{aligned}axe neutre F-G
\begin{aligned} &a_y=\infty\\ &a_x=-7,5 cm\\ &y=-\frac{i_x}{a_y}=0 cm\\ &x=-\frac{i_y}{a_x}=2,12 cm\\ \end{aligned}axe neutre G-A
\begin{aligned} &y-y_G=\frac{y_A-y_G}{x_A-x_G}\cdot (x-x_G)\\ &x_G=-7,5 cm, y_G=4,11 cm\\ &x_A=-4 cm, y_A=10,11 cm\\ &y=1,71x+16,96\\ &a_y=16,96 cm\\ &a_x=-9,89 cm\\ &y=-\frac{i_x}{a_y}=-1,39 cm\\ &x=-\frac{i_y}{a_x}=1,61 cm\\ \end{aligned}axe neutre A-B
\begin{aligned} &a_y=10,11 cm\\ &a_x=\infty\\ &y=-\frac{i_x}{a_y}=-2,33 cm\\ &x=-\frac{i_y}{a_x}=0 cm\\ \end{aligned}axe neutre B-D
\begin{aligned} &x_B=4 cm, y_B=10,11 cm\\ &x_D=7,5 cm, y_D=4,11 cm\\ &y=-1,71x+16,96\\ &a_y=16,96 cm\\ &a_x=9,89 cm\\ &y=-\frac{i_x}{a_y}=-1,39 cm\\ &x=-\frac{i_y}{a_x}=-1,61 cm\\ \end{aligned}Noyau de la section