Características geométricas, momentos de inercia centrados

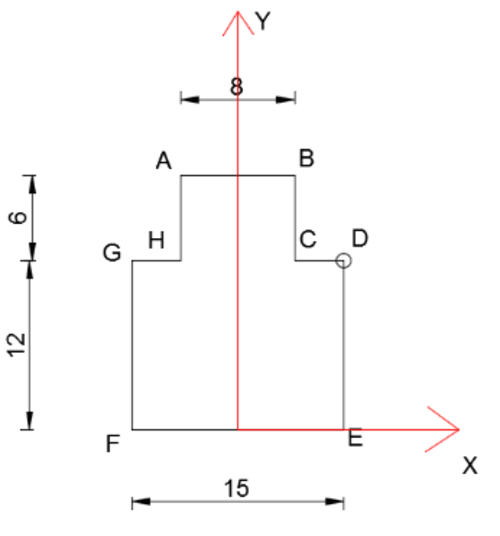
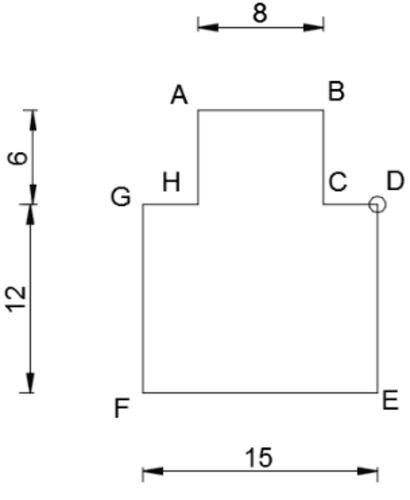
Figura 1 - rectángulo grande, Figura 2 - rectángulo pequeño

\begin{aligned} a&A_1 =180 cm^2\\ &A_2 =48 cm^2\\ &A=A_1 +A_2=228 cm^2\\ &y_1 =6 cm\\ &y_2 =15 cm\\ &y_c=\frac{y_1 ⋅A_1+ y_2 ⋅A_2}{A_1 +A_2}=7,89 cm\\ \end{aligned}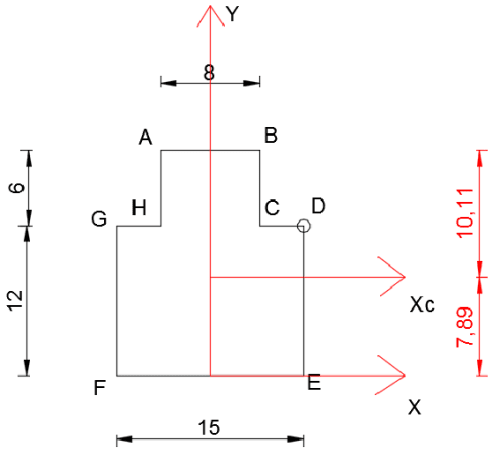 \begin{aligned} &I_{xc}=\frac{15\cdot 12^3}{12}+A_1\cdot (y_1-y_c)^2+\frac{8\cdot 6^3}{12}+A_2\cdot (y_2-y_c)^2=5373,47 cm^4\\ &I_{yc}=\frac{12\cdot 15^3}{12}+\frac{6\cdot 8^3}{12}=3631 cm^4\\ \end{aligned}

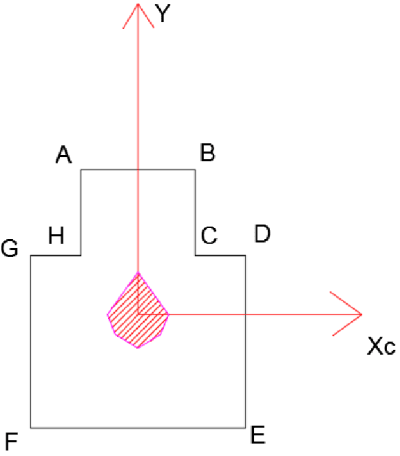
La fuerza en el punto D dirigida "detrás de la hoja" (compresión) crea momentos Mx y My en las direcciones mostradas en la imagen a continuación (regla de la mano derecha).

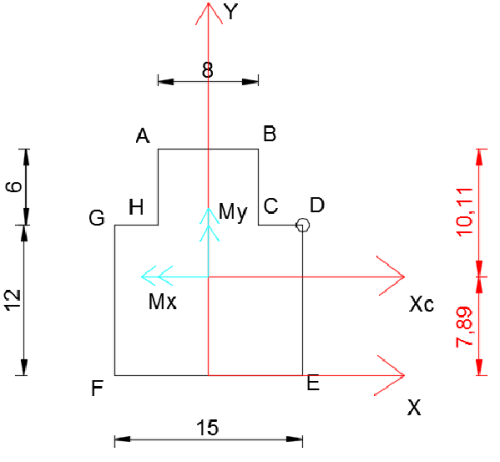
Determinación de la ecuación del eje neutro

\begin{aligned} &N=-60 kN\\ &M_y=-|N|\cdot 0,075=-4,5 kNm\\ &M_x=-|N|\cdot |(0,12-0,0789)|=-2,466 kNm\\ &\sigma_x=\frac{-60\cdot 10^3}{228\cdot 10^{-4}}-\frac{2,466\cdot 10^3}{5373,37\cdot 10^{-8}}y-\frac{4,5\cdot 10^3}{3631\cdot 10^{-8}}x=0\\ &y=-2,7x-5,7\\ \end{aligned}

Dos puntos arbitrarios definen una línea recta (eje neutro).

\begin{aligned} &x=1, y=-8,4\\ &x=-1, y=-3\\ \end{aligned}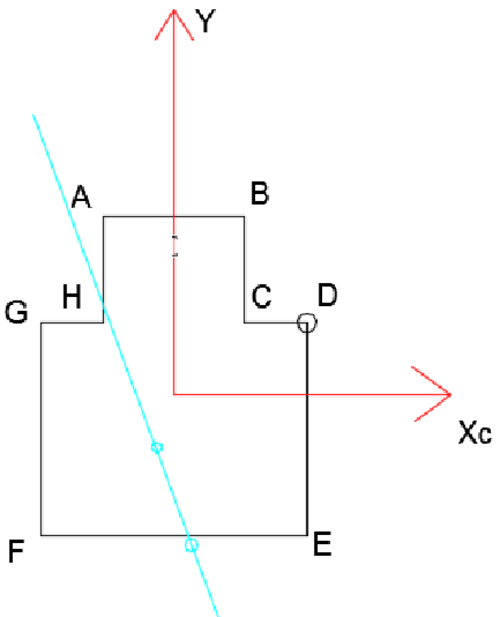

Esfuerzos en puntos característicos

\(\sigma=\frac{-60\cdot 10^3}{0.023}-\frac{2,466\cdot 10^3}{5373,37\cdot 10^{-8}}y-\frac{4,5\cdot 10^3}{3631\cdot 10^{-8}}x\)

Punto A (x=-4 cm, y=10,11 cm)

\(\sigma=-2,29 MPa\)

Punto B (x=4 cm, y=10,11 cm)

\(\sigma=-12,21 MPa\)

Punto C (x=4 cm, y=(12-7,89) cm)

\(\sigma=-9,45 MPa\)

Punto D (x=7,5 cm, y=(12-7,89) cm)

\(\sigma=-13,79 MPa\)

Punto E (x=7,5 cm, y=-7,89 cm)

\(\sigma=-8,28 MPa\)

Punto F (x=-7,5 cm, y=-7,89 cm)

\(\sigma=10,31 MPa\)

Punto G (x=-7,5 cm, y=(12-7,89) cm)

\(\sigma=4,8 MPa\)

Punto H (x=-4 cm, y=(12-7,89) cm)

\(\sigma=0,46 MPa\)

Cuerpo de tensiones

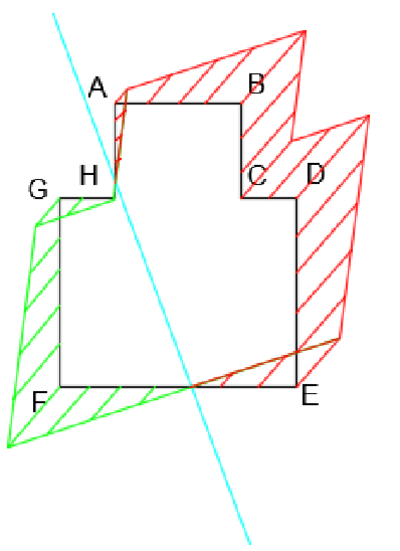
Núcleo de la sección

Marcamos las tangentes a la sección (en violeta), para cada tangente determinamos un punto de esquina del núcleo de la sección.

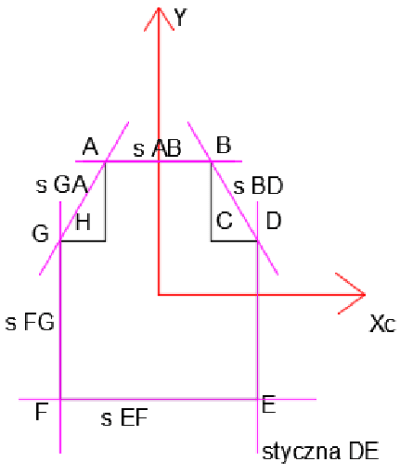\begin{aligned} &i_x^2=\frac{I_{xc}}{A}=23,57 cm^2\\ &i_y^2=\frac{I_{yc}}{A}=15,93 cm^2\\ \end{aligned}

Vamos a utilizar, entre otras cosas, la ecuación de la recta a través de dos puntos:

\begin{aligned} &y-y_1=\frac{y_2-y_1}{x_2-x_1}\cdot (x-x_1)\\ \end{aligned}

eje neutro D-E

\begin{aligned} &a_y=\infty\\ &a_x=7,5 cm\\ &y=-\frac{i_x}{a_y}=0 cm\\ &x=-\frac{i_y}{a_x}=-2,12 cm\\ \end{aligned}

eje neutro E-F

\begin{aligned} &a_y=-7,89 cm\\ &a_x=\infty\\ &y=-\frac{i_x}{a_y}=2,99 cm\\ &x=-\frac{i_y}{a_x}=0 cm\\ \end{aligned}

eje neutro F-G

\begin{aligned} &a_y=\infty\\ &a_x=-7,5 cm\\ &y=-\frac{i_x}{a_y}=0 cm\\ &x=-\frac{i_y}{a_x}=2,12 cm\\ \end{aligned}

eje neutro G-A

\begin{aligned} &y-y_G=\frac{y_A-y_G}{x_A-x_G}\cdot (x-x_G)\\ &x_G=-7,5 cm, y_G=4,11 cm\\ &x_A=-4 cm, y_A=10,11 cm\\ &y=1,71x+16,96\\ &a_y=16,96 cm\\ &a_x=-9,89 cm\\ &y=-\frac{i_x}{a_y}=-1,39 cm\\ &x=-\frac{i_y}{a_x}=1,61 cm\\ \end{aligned}

eje neutro A-B

\begin{aligned} &a_y=10,11 cm\\ &a_x=\infty\\ &y=-\frac{i_x}{a_y}=-2,33 cm\\ &x=-\frac{i_y}{a_x}=0 cm\\ \end{aligned}

eje neutro B-D

\begin{aligned} &x_B=4 cm, y_B=10,11 cm\\ &x_D=7,5 cm, y_D=4,11 cm\\ &y=-1,71x+16,96\\ &a_y=16,96 cm\\ &a_x=9,89 cm\\ &y=-\frac{i_x}{a_y}=-1,39 cm\\ &x=-\frac{i_y}{a_x}=-1,61 cm\\ \end{aligned}

Núcleo de la sección