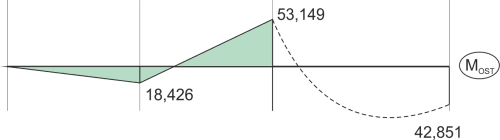
Solution
Dans cet exemple, nous montrerons comment résoudre la même poutre en utilisant deux configurations de base différentes.
MÉTHODE I
Nous calculons le degré d'indéterminisme statique SSN et sélectionnons la configuration de base de la méthode des forces UPMS.
SSN = 4-3 = 1
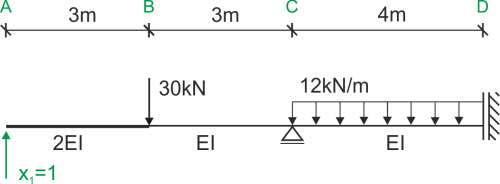
Nous dessinons le diagramme des unités et le diagramme de la charge externe.
État P
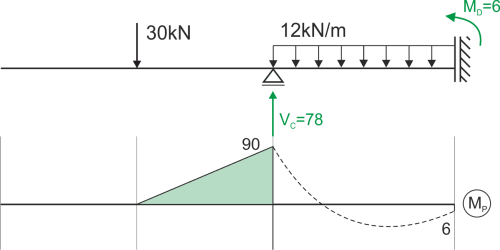 \begin{aligned} &\sum{F_{iY}}=0 & V_C=30+12\cdot4=78\ kN\\ &\sum{M_{C}}=0 & -M_D+12\cdot4\cdot2-30\cdot3=0 & \Longrightarrow M_D=6\ kNm\\ \end{aligned}
\begin{aligned} &\sum{F_{iY}}=0 & V_C=30+12\cdot4=78\ kN\\ &\sum{M_{C}}=0 & -M_D+12\cdot4\cdot2-30\cdot3=0 & \Longrightarrow M_D=6\ kNm\\ \end{aligned}
État x1=1
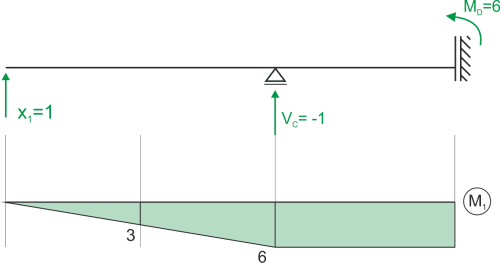
Nous calculons X1 et dessinons le diagramme du moment final.
Équation canonique de la méthode des forces
\(\delta_{11} \cdot x_1 + \Delta {_1}{_P}=0\)Nous calculons le coefficient et le terme constant de l'équation canonique.
\(\Delta{_1}{_P}=\)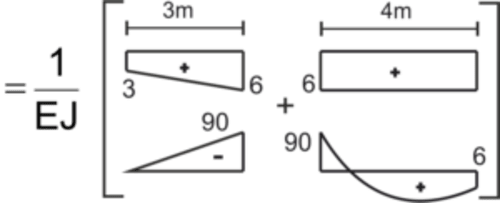 \(\Delta{_1}{_P}=\frac{1}{EI}(-\frac{1}{6}\cdot3\cdot90\cdot3-\frac{1}{3}\cdot90\cdot6\cdot3- \frac{1}{2}\cdot90\cdot6\cdot4+\frac{1}{2}\cdot6\cdot6\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot6)=-\frac{1299}{EI}\)
\(\delta_{{_1}{_1}}=\\\)
\(\Delta{_1}{_P}=\frac{1}{EI}(-\frac{1}{6}\cdot3\cdot90\cdot3-\frac{1}{3}\cdot90\cdot6\cdot3- \frac{1}{2}\cdot90\cdot6\cdot4+\frac{1}{2}\cdot6\cdot6\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot6)=-\frac{1299}{EI}\)
\(\delta_{{_1}{_1}}=\\\)
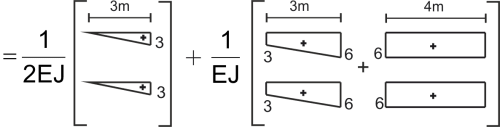 \( \delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot3\cdot3\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot6\cdot6\cdot3+\frac{1}{3}\cdot3\cdot3\cdot3+\frac{1}{6}\cdot3\cdot6\cdot3\cdot2+\cdot6\cdot6\cdot4)=\frac{211,5}{EI} \)
\( \delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot3\cdot3\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot6\cdot6\cdot3+\frac{1}{3}\cdot3\cdot3\cdot3+\frac{1}{6}\cdot3\cdot6\cdot3\cdot2+\cdot6\cdot6\cdot4)=\frac{211,5}{EI} \)
Nous résolvons l'équation canonique de la méthode des forces et calculons la réaction recherchée.
\(X_1=\frac{-\Delta{_1}{_P}}{\delta_{{_1}{_1}}}=6,142\)En utilisant la méthode de superposition, nous calculons les valeurs de moment sur le diagramme final.
\begin{aligned} &M_{OST}=M_1\cdot{X_1}+M_P\\ &M_A=0\\ &M_B=3\cdot{X_1}+0=18,426\\ &M_C=6\cdot{X_1}-90=-53,149\\ &M_D=6\cdot{X_1}+6=42,851\\ \end{aligned}Nous dessinons le diagramme final de moment fléchissant.
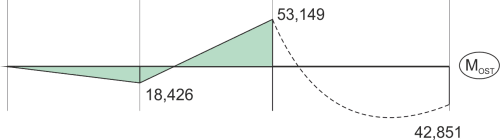
Commentaire sur la ligne en pointillé sous la charge continue (diagramme parabolique) :
En général, pour déterminer si le diagramme des moments parabolique atteindra une valeur extrême entre les points caractéristiques ou non, il est nécessaire de tracer le diagramme des forces tranchantes sur cet intervalle et de vérifier si le diagramme se croise. S'il se croise, alors il y aura un extremum sur le diagramme des moments à cet endroit. Cependant, dans ce cas spécifique, en regardant le support et la charge sur la poutre, nous pouvons voir que le diagramme des forces tranchantes ne change pas de signe entre ces points caractéristiques, car il commence par une valeur de 0 du côté droit (absence de force tranchante initiale) et ne change que dans une seule direction sur cet intervalle (charge continue). Cependant, pour le cas général à ce stade, nous ne pouvons pas dire s'il y aura un extrémum, je suggère donc soit de ne pas tracer de parabole avant de calculer s'il y aura un extrémum, soit de la dessiner en utilisant une ligne en pointillé. Ce sont néanmoins des observations assez lâches et différentes opinions peuvent être trouvées à ce sujet.
Étant donné que l'objectif de l'énoncé était simplement de tracer le diagramme Most, les forces tranchantes ne sont pas calculées dans cet exemple.
MÉTHODE II
Nous calculons le degré d'indéterminisme statique SSN et sélectionnons la configuration de base de la méthode des forces UPMS.
SSN = 4-3 = 1
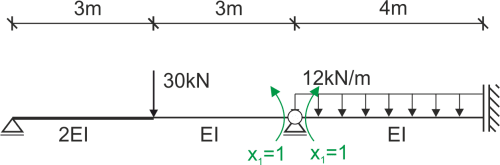
Nous dessinons le diagramme des unités et le diagramme de la charge externe.
État P
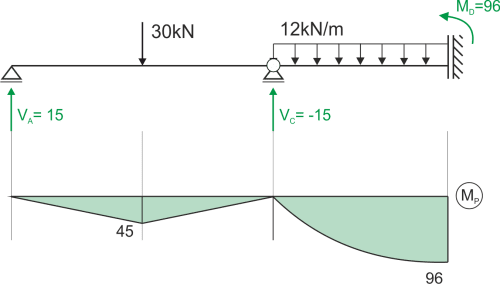 \begin{aligned}
&\sum{M_{C}}=0 & 12\cdot4\cdot2-M_D=0 & \Longrightarrow M_D=96\ kNm\\
&\sum{M_{A}}=0 & 30\cdot3-V_C\cdot6=0 & \Longrightarrow V_C=15\ kN\\
&\sum{F_{iY}}=0 & V_A+V_C-30=0 & \Longrightarrow V_A=15\ kN\\
\end{aligned}
\begin{aligned}
&\sum{M_{C}}=0 & 12\cdot4\cdot2-M_D=0 & \Longrightarrow M_D=96\ kNm\\
&\sum{M_{A}}=0 & 30\cdot3-V_C\cdot6=0 & \Longrightarrow V_C=15\ kN\\
&\sum{F_{iY}}=0 & V_A+V_C-30=0 & \Longrightarrow V_A=15\ kN\\
\end{aligned}
État x1=1
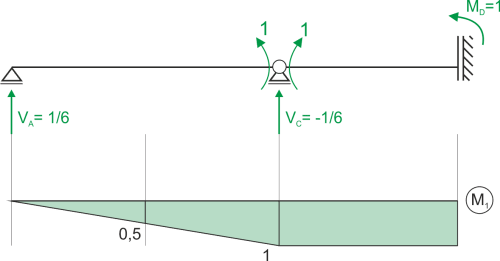
Nous calculons X1 et dessinons le diagramme du moment final.
Nous calculons le coefficient et le terme constant de l'équation canonique.
\(\Delta{_1}{_P}= \)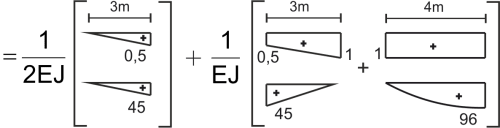 \( \Delta{_1}{_P}=\frac{1}{2EI}(\frac{1}{3}\cdot45\cdot0,5\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot0,5\cdot45\cdot3 +\frac{1}{6}\cdot1\cdot45\cdot3+\frac{1}{2}\cdot96\cdot1\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot1)=\frac{312,25}{EI} \)
\(\delta_{{_1}{_1}}=\)
\( \Delta{_1}{_P}=\frac{1}{2EI}(\frac{1}{3}\cdot45\cdot0,5\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot0,5\cdot45\cdot3 +\frac{1}{6}\cdot1\cdot45\cdot3+\frac{1}{2}\cdot96\cdot1\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot1)=\frac{312,25}{EI} \)
\(\delta_{{_1}{_1}}=\)
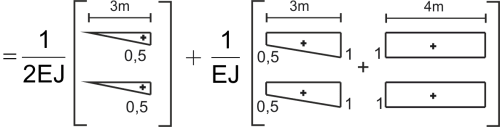 \(\delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot0,5^2\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot1^2\cdot3+\frac{1}{3}\cdot0,5^2\cdot3+\frac{1}{6}\cdot1\cdot0,5\cdot2\cdot3+1^2\cdot4)=\frac{5,875}{EI}\)
\(\delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot0,5^2\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot1^2\cdot3+\frac{1}{3}\cdot0,5^2\cdot3+\frac{1}{6}\cdot1\cdot0,5\cdot2\cdot3+1^2\cdot4)=\frac{5,875}{EI}\)
Nous résolvons l'équation canonique de la méthode des forces et calculons la réaction recherchée.
\(X_1=-53,149\)En utilisant la méthode de superposition, nous calculons les valeurs de moment sur le diagramme final.
\begin{aligned} &M_{OST}=M_1\cdot{X_1}+M_P\\ &M_A=0\\ &M_B=0,5\cdot{X_1}+45=18,426\\ &M_C=1\cdot{X_1}+0=-53,149\\ &M_D=1\cdot{X_1}+96=42,851\\ \end{aligned}