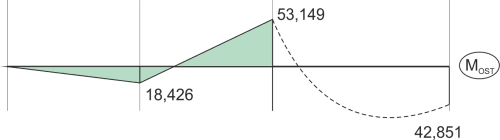
Solución
En este ejemplo mostraremos cómo resolver la misma viga utilizando dos configuraciones básicas diferentes.
MÉTODO I
Calculamos el grado de indeterminación estática GIE y seleccionamos la configuración básica del método de fuerzas UPMS.
GIE = 4-3 = 1
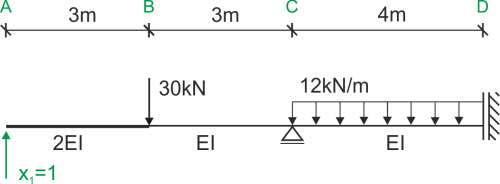
Dibujamos el diagrama unitario y el diagrama de la carga externa.
Estado P
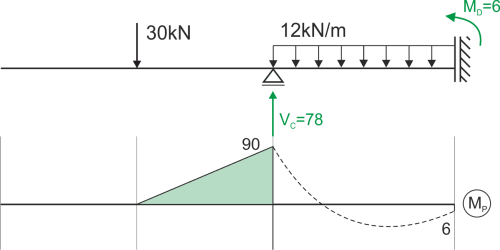 \begin{aligned} &\sum{F_{iY}}=0 & V_C=30+12\cdot4=78\ kN\\ &\sum{M_{C}}=0 & -M_D+12\cdot4\cdot2-30\cdot3=0 & \Longrightarrow M_D=6\ kNm\\ \end{aligned}
\begin{aligned} &\sum{F_{iY}}=0 & V_C=30+12\cdot4=78\ kN\\ &\sum{M_{C}}=0 & -M_D+12\cdot4\cdot2-30\cdot3=0 & \Longrightarrow M_D=6\ kNm\\ \end{aligned}
Estado x1 = 1
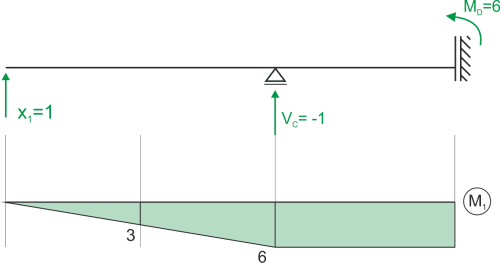
Calculamos X1 y trazamos el diagrama de momento final.
Ecuación canónica del método de fuerzas
\(\delta_{11} \cdot x_1 + \Delta {_1}{_P}=0\)Calculamos el coeficiente y el término independiente de la ecuación canónica.
\(\Delta{_1}{_P}=\)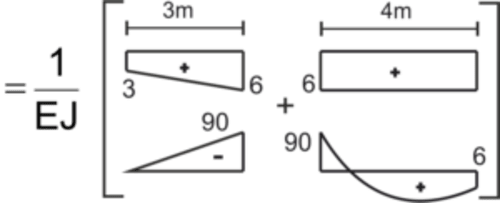 \(\Delta{_1}{_P}=\frac{1}{EI}(-\frac{1}{6}\cdot3\cdot90\cdot3-\frac{1}{3}\cdot90\cdot6\cdot3- \frac{1}{2}\cdot90\cdot6\cdot4+\frac{1}{2}\cdot6\cdot6\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot6)=-\frac{1299}{EI}\)
\(\delta_{{_1}{_1}}=\\\)
\(\Delta{_1}{_P}=\frac{1}{EI}(-\frac{1}{6}\cdot3\cdot90\cdot3-\frac{1}{3}\cdot90\cdot6\cdot3- \frac{1}{2}\cdot90\cdot6\cdot4+\frac{1}{2}\cdot6\cdot6\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot6)=-\frac{1299}{EI}\)
\(\delta_{{_1}{_1}}=\\\)
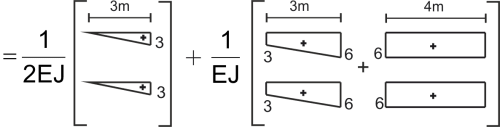 \( \delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot3\cdot3\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot6\cdot6\cdot3+\frac{1}{3}\cdot3\cdot3\cdot3+\frac{1}{6}\cdot3\cdot6\cdot3\cdot2+\cdot6\cdot6\cdot4)=\frac{211,5}{EI} \)
\( \delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot3\cdot3\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot6\cdot6\cdot3+\frac{1}{3}\cdot3\cdot3\cdot3+\frac{1}{6}\cdot3\cdot6\cdot3\cdot2+\cdot6\cdot6\cdot4)=\frac{211,5}{EI} \)
Resolvemos la ecuación canónica del método de fuerzas y calculamos la reacción buscada.
\(X_1=\frac{-\Delta{_1}{_P}}{\delta_{{_1}{_1}}}=6,142\)Utilizando el método de superposición, calculamos los valores del momento en el diagrama final.
\begin{aligned} &M_{OST}=M_1\cdot{X_1}+M_P\\ &M_A=0\\ &M_B=3\cdot{X_1}+0=18,426\\ &M_C=6\cdot{X_1}-90=-53,149\\ &M_D=6\cdot{X_1}+6=42,851\\ \end{aligned}Dibujamos el diagrama final del momento flexionante.
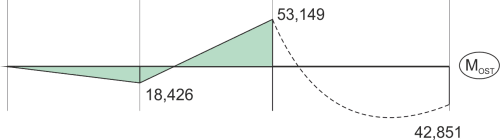
Comentario sobre la línea discontinua debajo de la carga continua (diagrama parabólico):
En general, para determinar si en el diagrama de momentos paraboloidal entre los puntos característicos hay un valor extremal o no, se debe trazar el diagrama de cortante en ese tramo y determinar si se anula en el diagrama de cortante. Si se anula, entonces habrá un extremo en ese punto en el diagrama de momentos. En este caso particular, utilizando nuestra intuición y mirando el apoyo y la carga de la viga, podemos ver que el diagrama de cortante ciertamente no cambia de signo entre esos puntos característicos, ya que comienza desde cero en el lado derecho (sin fuerza de corte inicial) y solo cambia en una dirección en ese tramo (carga continua). Sin embargo, para un caso general en esta etapa no tenemos forma de determinar si habrá un extremo, por lo que sugiero no dibujar la parábola hasta que se calcule si habrá un extremo, o dibujarla con una línea discontinua. Estas son observaciones bastante informales y puede haber diferentes opiniones al respecto.
Dado que según el enunciado del problema el objetivo era solo el diagrama de momentos, no se calculan las fuerzas cortantes en este problema.
MÉTODO II
Calculamos el grado de indeterminación estática GIE y seleccionamos la configuración básica del método de fuerzas UPMS.
GIE = 4-3 = 1
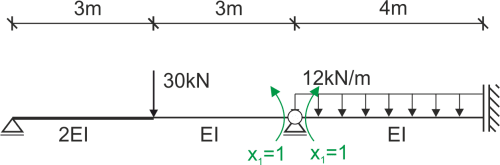
Dibujamos el diagrama unitario y el diagrama de la carga externa.
Estado P
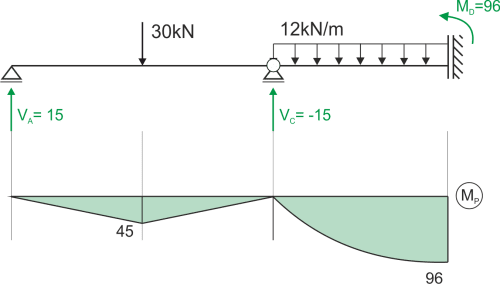 \begin{aligned}
&\sum{M_{C}}=0 & 12\cdot4\cdot2-M_D=0 & \Longrightarrow M_D=96\ kNm\\
&\sum{M_{A}}=0 & 30\cdot3-V_C\cdot6=0 & \Longrightarrow V_C=15\ kN\\
&\sum{F_{iY}}=0 & V_A+V_C-30=0 & \Longrightarrow V_A=15\ kN\\
\end{aligned}
\begin{aligned}
&\sum{M_{C}}=0 & 12\cdot4\cdot2-M_D=0 & \Longrightarrow M_D=96\ kNm\\
&\sum{M_{A}}=0 & 30\cdot3-V_C\cdot6=0 & \Longrightarrow V_C=15\ kN\\
&\sum{F_{iY}}=0 & V_A+V_C-30=0 & \Longrightarrow V_A=15\ kN\\
\end{aligned}
Estado x1 = 1
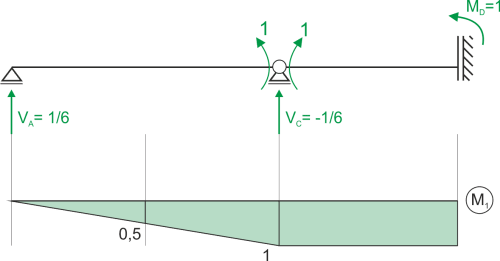
Calculamos X1 y trazamos el diagrama de momento final.
Calculamos el coeficiente y el término independiente de la ecuación canónica.
\(\Delta{_1}{_P}= \)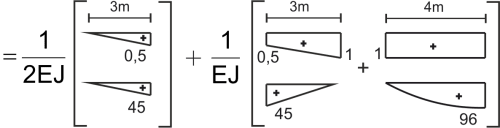 \( \Delta{_1}{_P}=\frac{1}{2EI}(\frac{1}{3}\cdot45\cdot0,5\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot0,5\cdot45\cdot3 +\frac{1}{6}\cdot1\cdot45\cdot3+\frac{1}{2}\cdot96\cdot1\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot1)=\frac{312,25}{EI} \)
\(\delta_{{_1}{_1}}=\)
\( \Delta{_1}{_P}=\frac{1}{2EI}(\frac{1}{3}\cdot45\cdot0,5\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot0,5\cdot45\cdot3 +\frac{1}{6}\cdot1\cdot45\cdot3+\frac{1}{2}\cdot96\cdot1\cdot4+\frac{2}{3}\cdot\frac{12\cdot4^{2}}{8}\cdot4\cdot1)=\frac{312,25}{EI} \)
\(\delta_{{_1}{_1}}=\)
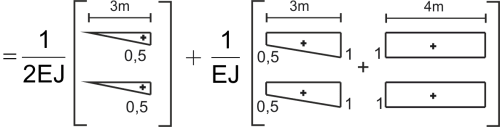 \(\delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot0,5^2\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot1^2\cdot3+\frac{1}{3}\cdot0,5^2\cdot3+\frac{1}{6}\cdot1\cdot0,5\cdot2\cdot3+1^2\cdot4)=\frac{5,875}{EI}\)
\(\delta_{{_1}{_1}}=\frac{1}{2EI}(\frac{1}{3}\cdot0,5^2\cdot3)+\frac{1}{EI}(\frac{1}{3}\cdot1^2\cdot3+\frac{1}{3}\cdot0,5^2\cdot3+\frac{1}{6}\cdot1\cdot0,5\cdot2\cdot3+1^2\cdot4)=\frac{5,875}{EI}\)
Resolvemos la ecuación canónica del método de fuerzas y calculamos la reacción buscada.
\(X_1=-53,149\)Utilizando el método de superposición, calculamos los valores del momento en el diagrama final.
\begin{aligned} &M_{OST}=M_1\cdot{X_1}+M_P\\ &M_A=0\\ &M_B=0,5\cdot{X_1}+45=18,426\\ &M_C=1\cdot{X_1}+0=-53,149\\ &M_D=1\cdot{X_1}+96=42,851\\ \end{aligned}