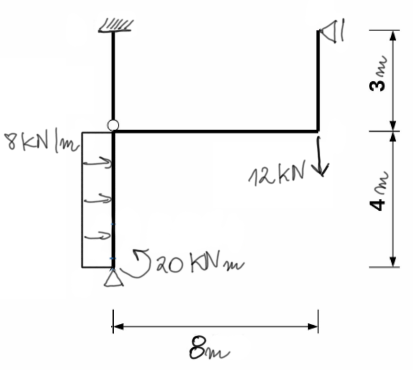
Solution

|
Nous calculons le degré d'indétermination statique SSN et choisissons la configuration de base de la méthode des forces UPMS. SSN=6-3-1=2En termes de degré d'indétermination statique, cet exemple est un peuspécifique, car nous avons deux réactions verticales le long de la barre AC. C'est donc une indétermination axiale, que nous ne résoudrons pas par la méthode des forces, mais nous la résoudrons seulement au stade du calcul des forces normales à partir de la condition géométrique. Néanmoins, nous résoudrons ce système comme étant doublement indéterminé, cependant, comme nous allons le voir tout de suite, un état unitaire sera nul, donc comme si nous calculions le système avec SSN=1. |
UPMS

Nous traçons les diagrammes unitaires et le diagramme de la charge externe.
État X1=1

État X2=1

État P

Si vous avez des problèmes pour dessiner les diagrammes de moments, nous vous encourageons à consulter cette vidéo de cours (CLIQUEZ)
Nous calculons les coefficients et les termes libres de l'équation canonique de la méthode des forces
Pour plus d'informations sur l'intégration, vous trouverez notre Introduction théorique sur ce sujet\begin{aligned} & \delta_{11}=\frac{1}{\mathrm{EI}} \cdot(0) \\ & \delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{12}{7} \cdot \frac{12}{7} \cdot 4+\frac{12}{7} \cdot \frac{12}{7} \cdot 8+\frac{1}{3} \cdot \frac{12}{7} \cdot \frac{12}{7} \cdot 3+\frac{1}{3} \cdot 3 \cdot 3 \cdot 3\right)=\frac{1929}{49} \frac{1}{\mathrm{EI}} \\ & \delta_{12}=\frac{1}{\mathrm{EI}} \cdot(0) \quad \delta_{21}=\delta_{12} \\ & \Delta_{1P}=\frac{1}{\mathrm{EI}} \cdot(0) \\ \end{aligned}

\begin{aligned} & \Delta_{2 P}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 36+\frac{1}{6} \cdot \frac{12}{7} \cdot 4 \cdot 20-\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 16+\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 36-\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 60-\frac{1}{3} \cdot \frac{12}{7} \cdot 3 \cdot 60\right) \\ & \Delta_{2 P}=-\frac{1392}{7} \frac{1}{\mathrm{EI}} \end{aligned}
Nous résolvons le système d'équations canoniques et calculons X1 et X2.
\begin{aligned} &\delta_{11}\cdot{x_1}+\delta_{12}\cdot{x_2}+\delta_{1P}=0 \\ &\delta_{21}\cdot{x_1}+\delta_{22}\cdot{x_2}+\delta_{2P}=0 \\ \end{aligned} \begin{aligned} & \left\{\begin{array}{l} 0 \cdot x_1+0 \cdot x_2+0=0 \\ 0 \cdot x_1+\frac{1929}{49 EI} \cdot x_2-\frac{1392}{7 EI}=0 \end{array}\right. \\ & \left\{\begin{array}{l} 0=0 \\ x_2=5,05 \mathrm{kN} \end{array}\right. \end{aligned}Nous calculons le moment final à partir de la formule de superposition
\begin{aligned} &M_{OST}=M_P+M_1\cdot{X_1}+M_2\cdot{X_2}\\ \end{aligned} Nous additionnons les diagrammes
Diagramme Pont

Calculs pour le diagramme des forces de cisaillement

|
\begin{aligned}
& \Sigma M_A=0 \\
& -20+44,657+8 \cdot 4 \cdot 2+ \\
& +Q_B \cdot 4=0 \\
& Q_B=-22,164 \mathrm{kN} \\
& \Sigma x=0 \\
& Q_B+8 \cdot 4-Q_A=0 \\
& Q_A=9,836 \mathrm{kN}
\end{aligned}
Extrême sur le diagramme des moments \begin{aligned} \frac{9,836}{x} & =\frac{22,164}{4-x} \\ x & =1,23 \mathrm{~m} \end{aligned} \begin{aligned} \text { Mex }=-20+Q_A \cdot x-8 \cdot \frac{x^2}{2}=-13,953 \mathrm{kNm} \end{aligned} |

\begin{aligned} & \Sigma M_B=0 \\ & Q_C \cdot 3+15,15=0 \\ & Q_C=-5,05 \mathrm{kN} \\ & \Sigma X=0 \\ & Q_B=Q_C \end{aligned} |

\begin{aligned} & \Sigma M_B=0 \\ & -44,657-51,343+ \\ & +Q_D \cdot 8=0 \\ & Q_D=12 \mathrm{kN} \\ & \Sigma y=0 \\ & Q_B=Q_D \end{aligned} |

\begin{aligned} & \Sigma M_D=0 \\ & 51,343+Q_E \cdot 3=0 \\ & Q_E=-17,114 \mathrm{kN} \\ & \Sigma x=0 \\ & Q_D=Q_E \end{aligned} |
Diagramme des forces de cisaillement

Calculs pour le diagramme des forces normales
Nœud B \begin{aligned} & \Sigma x=0 \\ & -5,05+22,164+ \\ & +N_{B D}=0 \\ & N_{B D}=-17,114 \mathrm{kN} \\ & \sum y=0 \\ & N_{B C}-12-N_{A B}=0 \\ & * N_{B C}=12+N_{A B} \\ \end{aligned} ici nous avons cette indétermination axiale dont nous avons parlé au début |
Nœud D \begin{gathered} \sum x=0(\text { spr.) } \\ -N_{B D}-17,114=0 \\ 0=0 \\ \Sigma y=0 \\ 12+N_{D E}-12=0 \\ N_{D E}=0 \mathrm{kN} \end{gathered} |
Solution de l'indétermination axiale (condition géométrique)
La force de cisaillement de 12 kN et sa direction nous indiquent dans quelle direction se déplacera le nœud B, et donc quel barreau sera étiré et lequel sera comprimé.L'allongement de la barre BC est égal au raccourcissement de la barre AB - et c'est la condition géométrique.
Rappelons-nous la formule pour l'allongement/raccourcissement d'une barre : \( \Delta_L = \frac{N\cdot L}{EA} \)

|
\begin{aligned} & \Delta L_{A B}=\Delta L_{B C} \\ & \frac{-N_{A B} \cdot 4}{E A}=\frac{N_{B C} \cdot 3}{E A} \\ & -4 N_{A B}=3 N_{B C} \\ & N_{A B}=-0,75 N_{B C} \\ & * N_{B C}=12-0,75 N_{B C} \\ & \left\{\begin{array}{l} N_{B C}=6,857 \mathrm{kN} \\ N_{A B}=-5,143 \mathrm{kN} \end{array}\right. \\ & \end{aligned} |
Diagramme final des forces normales

Vérification cinématique
\( \delta_i=\int \frac{Most \cdot \overline{M_i}}{EI} d S=0 \)
\begin{aligned} & \delta_2=\frac{1}{\mathrm{EI}} \cdot\left(\begin{array}{l} \frac{1}{3} \cdot 3 \cdot 3 \cdot 15 \cdot 15+\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 44.657+\frac{1}{6} \cdot \frac{12}{7} \cdot 4 \cdot 20-\frac{1}{3} \cdot \frac{12}{7} \cdot 4 \cdot 16+\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 44.657- \\ -\frac{1}{2} \cdot \frac{12}{7} \cdot 8 \cdot 51.343-\frac{1}{3} \cdot \frac{12}{7} \cdot 3 \cdot 51.343 \end{array}\right) \\ & \delta_2=-0.055 \frac{1}{\mathrm{EI}} \end{aligned} Erreur relative
\( \left|\frac{\delta_2}{\Delta_{2 p}}\right|=0.027 \% \quad<1,5 \% \)
Vérification statique
Nous lisons les réactions (valeurs et directions correctes) à partir des diagrammes des forces normales, de cisaillement et des moments fléchissants.Ensuite, nous écrivons les équations d'équilibre statique et vérifions si pour ces réactions lues, toutes les équations sont satisfaites.
 \begin{aligned}
& \Sigma \mathrm{x}=0 \\
& -5.05-17.114+8 \cdot 4-9.836=-0 \\
& \Sigma \mathrm{y}=0 \\
& 5.143+6.857-12=0 \\
& \Sigma \mathrm{M}_{\mathrm{D}}=0 \\
& -17.114 \cdot 3-5.05 \cdot 3+6.857 \cdot 8+15.15-8 \cdot 4 \cdot 2+9.836 \cdot 4+5.143 \cdot 8-20=0.002 \sim 0
\end{aligned}
\begin{aligned}
& \Sigma \mathrm{x}=0 \\
& -5.05-17.114+8 \cdot 4-9.836=-0 \\
& \Sigma \mathrm{y}=0 \\
& 5.143+6.857-12=0 \\
& \Sigma \mathrm{M}_{\mathrm{D}}=0 \\
& -17.114 \cdot 3-5.05 \cdot 3+6.857 \cdot 8+15.15-8 \cdot 4 \cdot 2+9.836 \cdot 4+5.143 \cdot 8-20=0.002 \sim 0
\end{aligned}
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.