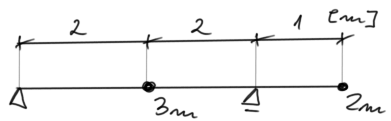
Solution

Degré d'indéterminisme statique
DIS=3-3=0Nombre de degrés de liberté dynamique
LDD=2
\( m_1=2m, m_2=3m \)
Graphiques des moments des forces unitaires appliquées aux degrés de liberté dynamique

Deltas dynamiques
\$$ \begin{aligned} &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 1 \cdot 1 \cdot 4+\frac{1}{3} \cdot 1 \cdot 1 \cdot 1\right)=\frac{5}{3} \cdot \frac{1}{\mathrm{EI}} \\ &\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 1 \cdot 1 \cdot 2+\frac{1}{3} \cdot 1 \cdot 1 \cdot 2\right)=\frac{4}{3} \cdot \frac{1}{\mathrm{EI}} \\ &\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{-1}{3} \cdot 0.5 \cdot 1 \cdot 2-\frac{1}{3} \cdot 0.5 \cdot 1 \cdot 2-\frac{1}{6} \cdot 1 \cdot 1 \cdot 2\right)=-1 \cdot \frac{1}{\mathrm{EI}} \end{aligned} \$$ Fréquences de vibrations (attention, il y a plusieurs approches pour calculer les fréquences de vibrations, voir plus dans l'introduction théorique - LIEN) \$$ \begin{aligned} &\mathrm{L}=\mathrm{m}_1 \cdot \delta_{11}+\mathrm{m}_2 \cdot \delta_{22}=\frac{22}{3} \cdot \frac{\mathrm{m}}{\mathrm{EI}} \\ &\mathrm{S}=2 \cdot \mathrm{m}_1 \cdot \mathrm{m}_2 \cdot\left(\delta_{11} \cdot \delta_{22}-\delta_{12}^2\right)=\frac{44}{3} \\ &\omega_1=\sqrt{\frac{\mathrm{L}-\sqrt{\mathrm{L}^2-2 \cdot \mathrm{S}}}{\mathrm{S}}}=0.404 \cdot \sqrt{\frac{\text { EI }}{\mathrm{m}}} \\ &\omega_2=\sqrt{\frac{\mathrm{L}+\sqrt{\mathrm{L}^2-2 \cdot \mathrm{S}}}{\mathrm{S}}}=0.915 \cdot \sqrt{\frac{\text { EI }}{\mathrm{m}}} \end{aligned} \$$ Après substitution des données \( EI=3,5\cdot 10^5 kNm^2 , m=750kg \) \$$ \begin{aligned} &\omega_1=0.404 \sqrt{\frac{3.5 \cdot 10^5 \cdot 10^3}{750}}=275.98 \cdot \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_2=0.915 \sqrt{\frac{3.5 \cdot 10^5 \cdot 10^3}{750}}=625.06 \cdot \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} \$$ Amplitudes des vibrations (plus d'informations sur l'approche du calcul des amplitudes des vibrations dans l'introduction - LIEN) \$$ A_2=\frac{1-\delta_{11} \cdot m_1 \cdot \omega^2}{\delta_{12} \cdot m_2 \cdot \omega^2} \cdot A_1 $$ je suppose \( \mathrm{A}_{11}=1 \quad pour \quad \omega_1=0.404 \sqrt{\frac{\text { EI }}{\mathrm{m}}} \) \$$ A_{21}=\frac{1-\frac{5}{3 E I} \cdot 2 \mathrm{~m} \cdot\left(0.404 \sqrt{\frac{E I}{m}}\right)^2}{\frac{-1}{E I} \cdot 3 \mathrm{~m} \cdot\left(0.404 \sqrt{\frac{E I}{m}}\right)^2} \cdot A_{11}=-0.931 $$ je suppose \( \mathrm{A}_{12}=1 \quad pour \quad \omega_2=0.915 \sqrt{\frac{\text { EI }}{m}} \) \$$ A_{22}=\frac{1-\frac{5}{3 \mathrm{EI}} \cdot 2 \mathrm{~m} \cdot\left(0.915 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2}{\frac{-1}{\mathrm{EI}} \cdot 3 \mathrm{~m} \cdot\left(0.915 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2} \cdot \mathrm{A}_{12}=0.713 $$ Condition d'orthogonalité \$$ A_{11} \cdot A_{12} \cdot m_1+A_{21} \cdot A_{22} \cdot m_2=0 $$ \( 1 \cdot 1 \cdot 2 m-0.931 \cdot 0.713 \cdot 3 m=0 \)
\( 0,009 m \sim 0 \)
Formes de vibrations


Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.