Solution
Voir introduction théorique à la méthode de Maxwell-Mohr ! Cela inclut également des conseils supplémentaires sur les exercices et les ressources liés à ce sujet!
En savoir plus sur l'intégration selon la méthode de Wereszczagina.
Solution du problème :
\begin{array}{lcc}
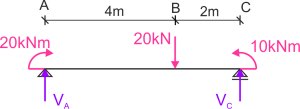
\sum M_{A}=0 & 20-10-6 V_{C}+20 \cdot 4=0 & V_{C}=15 k N \\
\sum M_{C}=0 & 20-10-20 \cdot 2+6 V_{A}=0 & V_{A}=5 k N \\
\sum Y=0 & V_{A}+V_{C}-20=0 & \mathrm{~L}=P
\end{array}
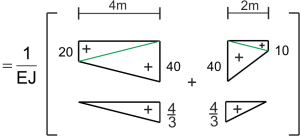 \begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
 \begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
En savoir plus sur l'intégration selon la méthode de Wereszczagina.
Solution du problème :
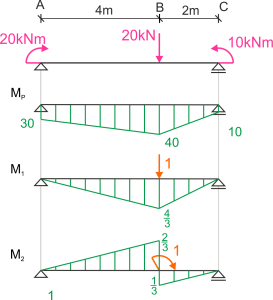
1. Dessiner le graphique des moments par rapport à la charge externe (Mp) ainsi que les graphiques unitaires M1 - poutre chargée par une force concentrée (pour calculer le déplacement vertical) et M2 - poutre chargée par un moment concentré (pour calculer l'angle de rotation).

2. Déplacement vertical du point B
\begin{aligned} \Delta_{B}=\int \frac{M_{P} \cdot M_{1}}{E J} d x= \end{aligned}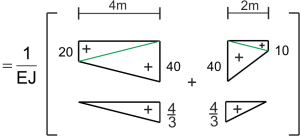 \begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
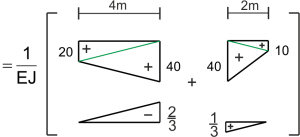
3. Angle de rotation du point B
\begin{aligned} \varphi_{B}=\int \frac{M_{P} \cdot M_{2}}{E J} d x= \end{aligned} \begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.