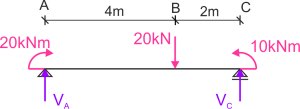
Solución
Ver introducción teórica al método de Maxwell-Mohr! ¡También incluye más ejercicios y materiales sobre este tema!
Aprende más sobre la integración por el método de Wereszczagina.
Solución del ejercicio:
\begin{array}{lcc}
\sum M_{A}=0 & 20-10-6 V_{C}+20 \cdot 4=0 & V_{C}=15 k N \\
\sum M_{C}=0 & 20-10-20 \cdot 2+6 V_{A}=0 & V_{A}=5 k N \\
\sum Y=0 & V_{A}+V_{C}-20=0 & \mathrm{~L}=P
\end{array}
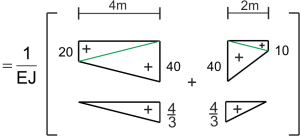 \begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
 \begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
Aprende más sobre la integración por el método de Wereszczagina.
Solución del ejercicio:
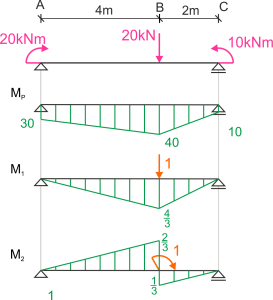
1. Graficar los momentos en función de la carga externa (Mp) y los momentos unitarios M1 - viga cargada con una fuerza concentrada (para calcular el desplazamiento vertical) y M2 - viga cargada con un momento concentrado (para calcular el ángulo de rotación).

2. Desplazamiento vertical del punto B
\begin{aligned} \Delta_{B}=\int \frac{M_{P} \cdot M_{1}}{E J} d x= \end{aligned}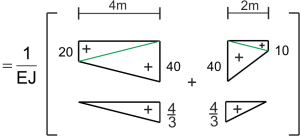 \begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[\frac{1}{6} \cdot 20 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{4}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{4}{3} \cdot 2\right]=\frac{128,89}{E J}
\end{aligned}
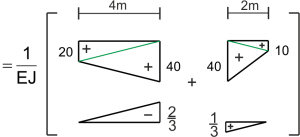
3. Ángulo de rotación del punto B
\begin{aligned} \varphi_{B}=\int \frac{M_{P} \cdot M_{2}}{E J} d x= \end{aligned} \begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
\begin{aligned}
=\frac{1}{E J}\left[-\frac{1}{6} \cdot 20 \cdot \frac{2}{3} \cdot 4-\frac{1}{3} \cdot 40 \cdot \frac{2}{3} \cdot 4+\frac{1}{3} \cdot 40 \cdot \frac{1}{3} \cdot 2+\frac{1}{6} \cdot 10 \cdot \frac{1}{3} \cdot 2\right]=-\frac{34,44}{E J}
\end{aligned}
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.