Solución
Solución YT
Versión clásica
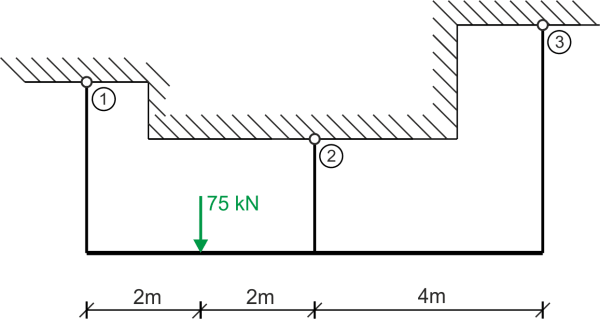
La suma de las fuerzas en el eje x no nos da ninguna información, por lo que tenemos dos ecuaciones efectivas de equilibrio estático. Las incógnitas son las fuerzas en las tres barras, por lo que el problema es estáticamente indeterminado una vez, para resolverlo debemos utilizar una condición adicional: la geométrica (del plano de desplazamientos).Ecuaciones de equilibrio:
\begin{aligned} &\sum{M_{C}}=0\\ &N_{1}\cdot 4 - 75\cdot 2 - N_{3}\cdot 4 = 0\\ &N_{1}=\frac{150 + 4\cdot N_{3}}{4}\\ &N_{1}=37,5 + N_{3}\\ &\sum{Y}=0\\ &N_{1} - 75 + N_{2} + N_{3} =0\\ &37,5 + N_{3} - 75 + N_{3}=-N_{2}\\ &N_{2}=37,5 - 2N_{3} \end{aligned}
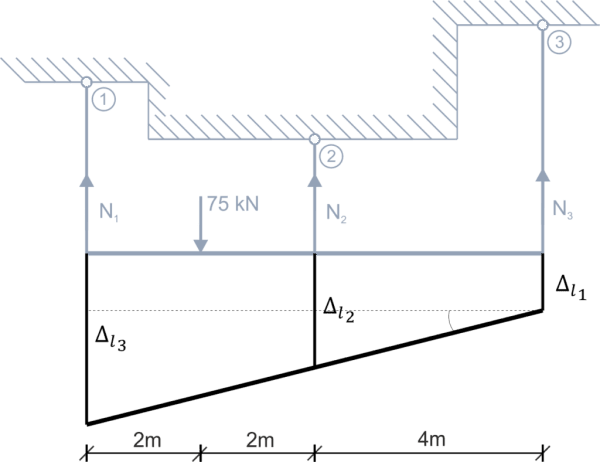
Condición geométrica \begin{aligned} &\frac{\Delta l_{3}-\Delta l_{1}}{8}=\frac{\Delta l_{2}-\Delta l_{1}}{4}\\ \end{aligned} Transformo y resuelvo la condición geométrica \begin{aligned} &\Delta l_{3}-\Delta l_{1}=2(\Delta l_{2}-\Delta l_{1})\\ &\Delta l_{3}+\Delta l_{1}-2\cdot \Delta l_{2}=0\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &\frac{N_{3}\cdot 4}{E_{3}\cdot A_{3}}+\frac{N_{1}\cdot 3}{E_{1}\cdot A_{1}}-2\cdot \frac{N_{2}\cdot 2}{E_{2}\cdot A_{2}}=0 \end{aligned} De los datos del problema: \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &\frac{E_{2}}{E_{1}}=\frac{105 \ GPa}{210 \ GPa}=\frac{1}{2} & \Rightarrow 2E_{2}=E_{1}\\ &E_{1}=E_{3}\\ \end{aligned} Sustituyo estas relaciones en la ecuación anterior \begin{aligned} &\frac{N_{3}\cdot 4}{2E_{2}\cdot A_{3}}+\frac{(37,5 + N_{3})\cdot 3}{2E_{2}\cdot 2A_{3}} - 2\cdot\frac{(37,5 - 2N_{3})\cdot 2}{E_{2}\cdot 2A_{3}}=0 & |\cdot E_{2}A_{3}\\ &2N_{3} + \frac{3}{4}(37,5 + N_{3}) - 2(37,5 - 2M_{3})=0\\ &2N_{3} + 28,125 + 0,75N_{3} - 75 + 2N_{3}\\ &4,75N_{3}=46,875\\ &N_{3}=9,868 \ kN \end{aligned} Regreso a las relaciones de las ecuaciones de equilibrio estático y calculo las fuerzas en las otras barras \begin{aligned} &N_{1}=37,5 + N_{3}=47,368 \ kN\\ &N_{2}=37,5 - 2N_{3}=17,764 \ kN\\ \end{aligned} Resuelvo la condición de resistencia para todas las barras \begin{aligned} &\sigma=\frac{N}{A}\\ &\sigma_{1}=\frac{47,368\cdot 10^{3}}{A_{1}}\le 120\cdot 10^{6} & \Rightarrow & A_{1}\ge 3,95\cdot 10^{-4} \ m^{2}\\ &\sigma_{2}=\frac{17,764\cdot 10^{3}}{A_{2}}\le 30\cdot 10^{6} & \Rightarrow & A_{2}\ge 5,92\cdot 10^{-4} \ m^{2}\\ &\sigma_{3}=\frac{9,868\cdot 10^{3}}{A_{3}}\le 120\cdot 10^{6} & \Rightarrow & A_{3}\ge 8,22\cdot 10^{-5} \ m^{2}\\ \end{aligned} Finalmente, tomo el área de la sección transversal de las barras recordando las relaciones dadas en el enunciado del problema: \begin{aligned} &A_{1}=A_{2}=2A_{3}\\ &A_{1}=A_{2}=6\cdot 10^{-4}\\ &A_{3}=\frac{1}{2}\cdot 6\cdot 10^{-4}=3\cdot 10^{-4}\\ \end{aligned} Calculo las tensiones en las barras para el área de sección transversal adoptada \begin{aligned} &\sigma_{1}=\frac{47,368\cdot 10^{3}}{6\cdot 10^{-4}}=78,95 \ MPa\\ &\sigma_{2}=\frac{17,764\cdot 10^{3}}{6\cdot 10^{-4}}=29,60 \ MPa\\ &\sigma_{3}=\frac{9,868\cdot 10^{3}}{3\cdot 10^{-4}}=32,89 \ MPa\\ \end{aligned}
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.