Solución
La figura no tiene eje de simetría, por lo que asumimos un sistema de ejes inicialmente arbitrario.
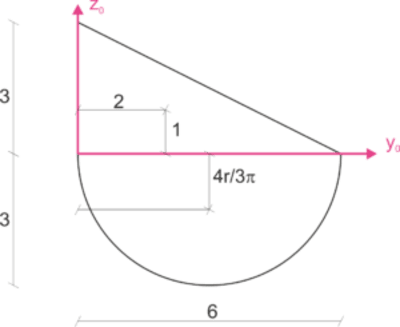
Buscamos las dos coordenadas del centro de gravedad. Las calculamos como la relación entre el momento estático de inercia y el área total de la sección. Es útil escribir las coordenadas "y" y "z" y las correspondientes áreas de gravedad de las figuras simples (y1, y2 y z1, z2) junto con sus áreas (A1 y A2).
Centro de gravedad
\[\begin{aligned} y_1=2[cm] & z_1=1[cm] & A_1=9cm^2\\ y_2=3[cm] & z_2=-\frac{4r}{3\pi}=-1.273[cm] & A_2=\frac{\pi r^2}{2}=14.137cm^2\\ \end{aligned}\] \[\begin{aligned} &A=A_1+A_2=23.14[cm^2]\\ &y_c=\frac{2*9+3*14.14}{23.14}=2.611[cm]\\ &z_c=\frac{1*9-1.273*14.14}{23.14}=-0.389[cm]\\ \end{aligned}\]Se marca el centro de gravedad calculado en el dibujo, los ejes se trasladan al centro de gravedad y se calculan los momentos centrales de inercia.
 \[\begin{aligned} &I_{yc}=\frac{6*3^3}{36}+9*(1-(-0.389))^2+[\frac{\pi r^4}{8}-\frac{8r^4}{9\pi}]+14.137*(-1.273-(-0.389))^2=41.808[cm^4]\\ &I_{zc}=\frac{6^3*3}{36}+9*(2-2.611)^2+\frac{\pi r^4}{8}+14.137*(3-2.611)^2=55.308[cm^4]\\ \end{aligned}\]
\[\begin{aligned} &I_{yc}=\frac{6*3^3}{36}+9*(1-(-0.389))^2+[\frac{\pi r^4}{8}-\frac{8r^4}{9\pi}]+14.137*(-1.273-(-0.389))^2=41.808[cm^4]\\ &I_{zc}=\frac{6^3*3}{36}+9*(2-2.611)^2+\frac{\pi r^4}{8}+14.137*(3-2.611)^2=55.308[cm^4]\\ \end{aligned}\]
Si tienes preguntas, comentarios, o crees que has encontrado un error en esta solución, por favor envíanos un mensaje a kontakt@edupanda.pl.
