The figure does not have a symmetry axis, so we assume an arbitrary axis arrangement.

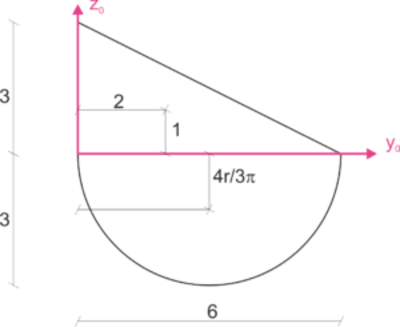
We are looking for two coordinates of the center of gravity. We calculate them as the ratio of the static moment of inertia to the total cross-sectional area. It is helpful to write down the "z-axis" and "y-axis" coordinates of the centers of gravity of individual simple figures (y1, y2, and z1, z2), as well as their areas (A1 and A2).

Center of Gravity

\begin{aligned} y_1=2 [cm] & z_1=1 [cm] & A_1=9cm^2\\ y_2=3 [cm] & z_2=-\frac{4r}{3\pi}=-1,273 [cm] & A_2=\frac{\pi r^2}{2}=14,137cm^2\\ \end{aligned} \begin{aligned} &A=A_1+A_2=23.14 [cm^2]\\ &y_c=\frac{2*9+3*14.14}{23.14}=2.611 [cm]\\ &z_c=\frac{1*9-1.273*14.14}{23.14}=-0.389 [cm]\\ \end{aligned}

We mark the calculated center of gravity on the diagram, the axes transferred to the center of gravity are the central axes. We calculate the central moments of inertia.

\begin{aligned} &I_{yc}=\frac{6*3^3}{36}+9*(1-(-0.389))^2+[\frac{\pi r^4}{8}-\frac{8r^4}{9\pi}]+14.137*(-1.273-(-0.389))^2=41.808 [cm^4]\\ &I_{zc}=\frac{6^3*3}{36}+9*(2-2.611)^2+\frac{\pi r^4}{8}+14.137*(3-2.611)^2=55.308 [cm^4]\\ \end{aligned}