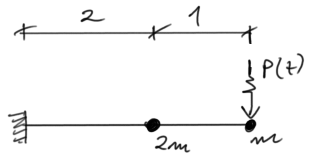
Solution
Degree of static indeterminacy
SSN=3-3=0Number of degrees of dynamic freedom
LSSD=2
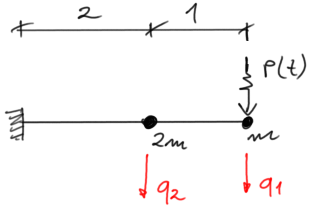
\( m_1=m\\ m_2=2m\)
Graphs of moments from unit forces applied at dynamic degrees of freedom
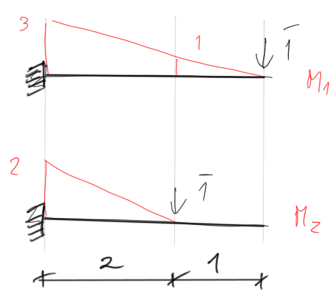
Dynamic deltas $$ \begin{aligned} &\delta_{11}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 3 \cdot 3 \cdot 3\right)=9 \cdot \frac{1}{\mathrm{EI}} \\ &\delta_{22}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 2 \cdot 2 \cdot 2\right)=\frac{8}{3} \cdot \frac{1}{\mathrm{EI}} \\ &\delta_{12}=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 3 \cdot 2 \cdot 2+\frac{1}{6} \cdot 1 \cdot 2 \cdot 2\right)=\frac{14}{3} \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ Vibration frequencies (note, there are several approaches to calculating vibration frequencies, more in the theoretical introduction - LINK) $$ \mathrm{L}=\mathrm{m}_1 \cdot \delta_{11}+\mathrm{m}_2 \cdot \delta_{22}=\frac{43}{3} \cdot \frac{\mathrm{m}}{\mathrm{EI}} $$ $$ \begin{aligned} &\mathrm{S}=2 \cdot \mathrm{m}_1 \cdot \mathrm{m}_2 \cdot\left(\delta_{11} \cdot \delta_{22}-\delta_{12}^2\right)=\frac{80}{9} \cdot\left(\frac{\mathrm{m}}{\mathrm{EI}}\right)^2 \\ &\omega_1=\sqrt{\frac{\mathrm{L}-\sqrt{\mathrm{L}^2-2 \cdot \mathrm{S}}}{\mathrm{S}}}=0.267 \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \\ &\omega_2=\sqrt{\frac{\mathrm{L}+\sqrt{\mathrm{L}^2-2 \cdot \mathrm{S}}}{\mathrm{S}}}=1.776 \cdot \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \end{aligned} $$ After substituting the data \( \quad \mathrm{EI}=2.1 \times 10^5 \cdot \mathrm{kNm}^2 \quad \mathrm{~m}=200 \mathrm{~kg} \) $$ \begin{aligned} &\omega_1=0.267 \sqrt{\frac{2.1 \cdot 10^5 \cdot 10^3}{200}}=273.59 \cdot \frac{\mathrm{rad}}{\mathrm{s}} \\ &\omega_2=1.776 \sqrt{\frac{2.1 \cdot 10^5 \cdot 10^3}{200}}=1819.86 \cdot \frac{\mathrm{rad}}{\mathrm{s}} \end{aligned} $$ Vibration amplitudes (more about the approach to calculating vibration amplitudes in the introduction - LINK) $$ \mathrm{A}_2=\frac{1-\delta_{11} \cdot \mathrm{m}_1 \cdot \omega^2}{\delta_{12} \cdot \mathrm{m}_2 \cdot \omega^2} \cdot \mathrm{A}_1 $$ assuming \( \quad \mathrm{A}_{11}=1 \quad for \quad \omega_1=0.267 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \) $$ \mathrm{A}_{21}=\frac{1-\frac{9}{\mathrm{EI}} \cdot 1 \mathrm{~m} \cdot\left(0.267 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2}{\frac{14}{3 \mathrm{EI}} \cdot 2 \mathrm{~m} \cdot\left(0.267 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2} \cdot \mathrm{A}_{11}=0.539 $$ assuming \( \quad \mathrm{A}_{12}=1 \quad for \quad \omega_2=1.776 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}} \) $$ \mathrm{A}_{22}=\frac{1-\frac{9}{\mathrm{EI}} \cdot 1 \mathrm{~m} \cdot\left(1.776 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2}{\frac{14}{3 \mathrm{EI}} \cdot 2 \mathrm{~m} \cdot\left(1.776 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2} \cdot \mathrm{A}_{12}=-0.93 $$ Orthogonality condition $$ \mathrm{A}_{11} \cdot \mathrm{A}_{12} \cdot \mathrm{m}_1+\mathrm{A}_{21} \cdot \mathrm{A}_{22} \cdot \mathrm{m}_2=0 $$ \( 1 \cdot 1 \cdot 1 \mathrm{~m}+0.539 \cdot(-0.93) \cdot 2 \mathrm{~m}=0 \)
\( -0,002 m \sim 0 \)
condition satisfied.
Modes of vibration
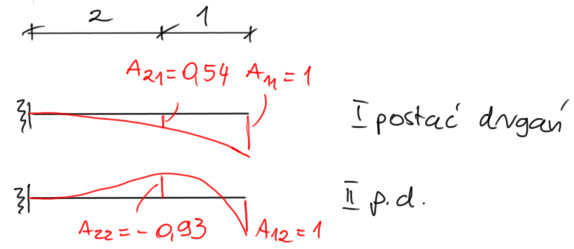
Inertial forces (see theoretical introduction) $$ \begin{aligned} &\delta_{11 \mathrm{~B}} \cdot \mathrm{B}_1+\delta_{12} \cdot \mathrm{B}_2+\Delta_{1 \mathrm{p}}=0 \\ &\delta_{21} \cdot \mathrm{B}_1+\delta_{22 \mathrm{~B}} \cdot \mathrm{B}_2+\Delta_{2 \mathrm{p}}=0 \end{aligned} $$ Forcing frequency $$ \begin{aligned} &\theta=\frac{\omega_1+\omega_2}{2} \\ &\theta=\frac{1}{2}\left(0.267 \sqrt{\frac{\text { EI }}{m}}+1.776 \sqrt{\frac{\text { EI }}{m}}\right)=1.022 \cdot \sqrt{\frac{\text { EI }}{m}} \end{aligned} $$ Inertial deltas $$ \begin{aligned} &\delta_{11 \mathrm{~B}}=\delta_{11}-\frac{1}{\mathrm{~m}_1 \cdot \theta^2} \\ &\delta_{11 \mathrm{~B}}=\frac{9}{\mathrm{EI}}-\frac{1}{\mathrm{~m} \cdot\left(1.022 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2}=8.043 \cdot \frac{1}{\mathrm{EI}} \\ &\delta_{22 \mathrm{~B}}=\delta_{22}-\frac{1}{\mathrm{~m}_2 \cdot \theta^2} \\ &\delta_{22 \mathrm{~B}}=\frac{8}{3 \mathrm{EI}}-\frac{1}{2 \mathrm{~m} \cdot\left(1.022 \sqrt{\frac{\mathrm{EI}}{\mathrm{m}}}\right)^2}=2.188 \cdot \frac{1}{\mathrm{EI}} \\ &\Delta_{1 \mathrm{p}}=\delta_{11} \cdot \mathrm{P}_{01}+\delta_{12} \cdot \mathrm{P}_{02} \\ &\Delta_{2 \mathrm{p}}=\delta_{21} \cdot \mathrm{P}_{01}+\delta_{22} \cdot \mathrm{P}_{02} \\ &\text{where:} \\ &\mathrm{P}_{01}=\mathrm{P}=10 \cdot \mathrm{kN} \quad \text{- forcing force on q1 direction} \\ &\mathrm{P}_{02}=0 \quad \text{- forcing force on q2 direction} \\ \end{aligned} $$ $$ \begin{aligned} &\Delta_{1 \mathrm{p}}=\frac{9}{\mathrm{EI}} \cdot \mathrm{P}_{01}+\frac{14}{3 \mathrm{EI}} \cdot \mathrm{P}_{02}=90 \cdot \frac{1}{\mathrm{EI}} \\ &\Delta_{2 \mathrm{p}}=\frac{14}{3 \mathrm{EI}} \cdot \mathrm{P}_{01}+\frac{8}{3 \mathrm{EI}} \cdot \mathrm{P}_{02}=46.667 \cdot \frac{1}{\mathrm{EI}} \end{aligned} $$ Solution of the system of equations, calculation of inertial forces $$ \begin{aligned} &\frac{8.043}{\mathrm{EI}} \cdot \mathrm{B}_1+\frac{14}{3 \mathrm{EI}} \cdot \mathrm{B}_2+\frac{90}{\mathrm{EI}}=0 \\ &\frac{14}{3 \mathrm{EI}} \cdot \mathrm{B}_1+\frac{2.188}{\mathrm{EI}} \cdot \mathrm{B}_2+\frac{46.667}{\mathrm{EI}}=0 \end{aligned} $$ $$ \begin{aligned} &\mathrm{B}_1=-4.99 \cdot \mathrm{kN} \\ &\mathrm{B}_2=-10.68 \cdot \mathrm{kN} \end{aligned} $$ Force diagram
On the force diagram, we mark the load on the frame from the forcing force, the weight of the masses and the calculated inertial forces.
Since the motion of the forcing force is sinusoidal, it means that in extreme cases the force is displaced in one direction or the other with its full value.
We mark this on the diagram, where on the first diagram we mark the direction consistent with the one given in the topic, and on the second diagram the opposite direction.
Then we mark the inertial forces - on the first diagram, the directions of the inertial forces are consistent with the initially assumed directions of q1 and q2 (see the initial drawing); on the second diagram, the directions are opposite (they change the direction just like the forcing force).
Once again - regardless of whether B1 and B2 came out as positive or negative, we mark the directions as described above. The sign of the inertial forces determines whether a given direction remains (if the force is positive) or should be changed (if the force is negative).
Weight from the masses - to calculate it, we multiply the mass by the acceleration due to gravity g. Directions on both diagrams are consistent with gravity - vertically downwards.
$$ \mathrm{mg}=0.200 \cdot 9.81=1.96 \cdot \mathrm{kN} $$
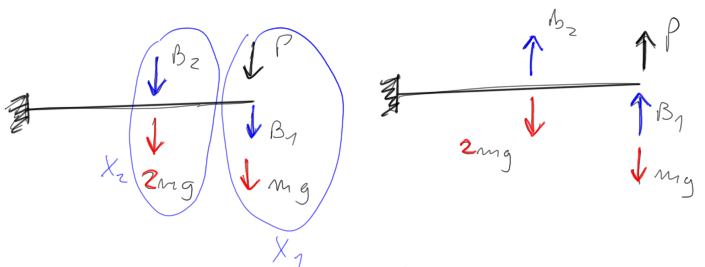
\begin{aligned} &\left\{\begin{array} { l } { \mathrm { x } _ { 1 } = \mathrm { P } + \mathrm { B } _ { 1 } + \mathrm { mg } } \\ { \mathrm { x } _ { 2 } = \mathrm { B } _ { 2 } + 2 \mathrm { mg } } \end{array} \left\{\begin{array}{l} \mathrm{x}_1=-\mathrm{P}-\mathrm{B}_1+\mathrm{mg} \\ \mathrm{x}_2=-\mathrm{B}_2+2 \mathrm{mg} \end{array}\right.\right.\\ \\ \\ &\left\{\begin{array} { l } { \mathrm { x } _ { 1 } = 6 . 9 7 2 \mathrm { kN } } \\ { \mathrm { x } _ { 2 } = - 6 . 7 5 6 \mathrm { kN } } \end{array} \quad \left\{\begin{array}{l} \mathrm{x}_1=-3.048 \mathrm{kN} \\ \mathrm{x}_2=14.604 \mathrm{kN} \end{array}\right.\right. \end{aligned}
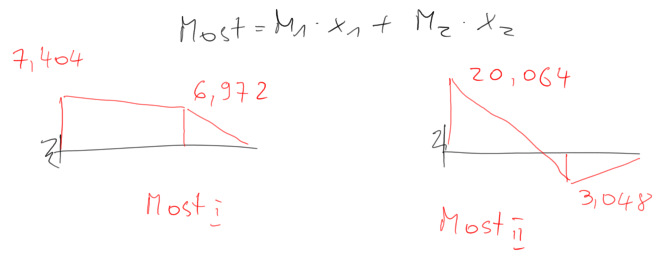
If you have any questions, comments, or think you have found a mistake in this solution, please send us a message at kontakt@edupanda.pl.