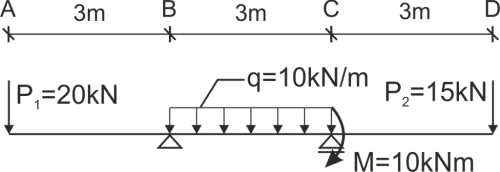
Rozwiązanie
Uwaga – w zrozumieniu tego przykładu może pomóc przeczytanie wstępu teoretycznego oraz obejrzenie wideo-kursu poniżej:
Rozwiązanie klasyczne
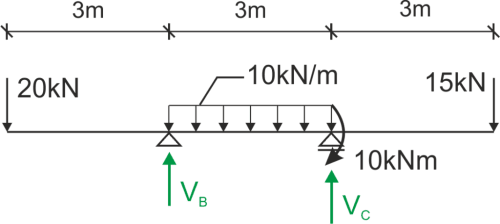
Obliczamy reakcje podporowe
 \begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
\begin{aligned} &\sum{M_B}=0 -20\cdot 3+30\cdot 1.5+10+15\cdot 6-R_C\cdot 3=0 R_A=28.33kN\\ &\sum{M_C}=0 -20\cdot 6+R_B\cdot 3-30\cdot 1.5+10+15\cdot 3=0 R_B=36.67kN\\ &\sum{P_iY}=0 -20+R_B-30+R_C-15=0 L=P\\ \end{aligned}
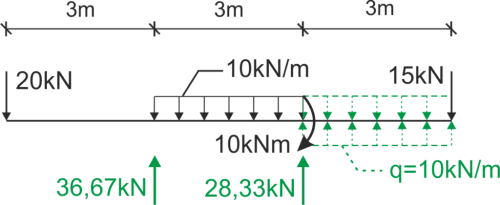
Zapisujemy funkcję momentu od lewej strony.
Funkcję można też zapisać z prawej strony. Zachęcamy do sprawdzenia tego wariantu, obliczenia szukanego przemieszczenia i porównania wyników.
 \begin{aligned} &M_g=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJW"=-M_g\\ &-M_g=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJW'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJW=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\ \end{aligned}
\begin{aligned} &M_g=-20x+R_B(x-3)-\frac{1}{2}q(x-3)^2+R_C(x-6)+10(x-6)^0+\frac{1}{2}q(x-6)^2\\ &EJW"=-M_g\\ &-M_g=20x-R_B(x-3)+5(x-3)^2- 28.33(x-6)-10(x-6)^0-5(x-6)^2\\ &EJW'=20\frac{x^2}{2}-36.67\frac{(x-3)^2}{2}+5\frac{(x-3)^3}{3}-28.33\frac{(x-6)^2}{2}-10(x-6)-5\frac{(x-6)^3}{3}+C\\ &EJW=20\frac{x^3}{6}-36.67\frac{(x-3)^3}{6}+5\frac{(x-3)^4}{12}-28.33\frac{(x-6)^3}{6}-10\frac{(x-6)^2}{2}-5\frac{(x-6)^4}{12}+Cx+D\\ \end{aligned}
Warunki brzegowe
\begin{aligned} &W(3)=0 ---> 90+3C+D=0\\ &w(6)=0---> 588.735+6C+D=0\\ &C=-166,245\\ &D=408.735\\ \end{aligned}Obliczamy ugięcie w punkcie A.
\begin{aligned} &W_A=\frac{1}{EI}\cdot (408.735)\\ \end{aligned}
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: