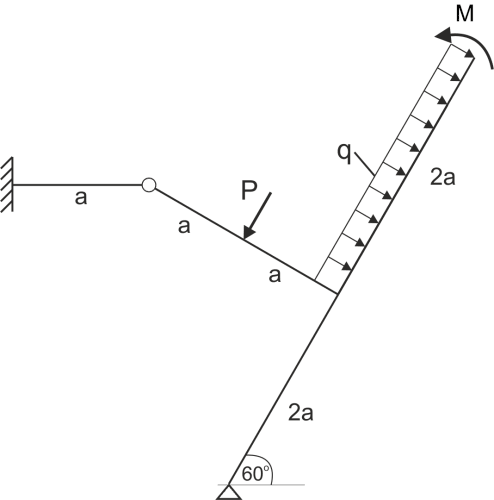
Rozwiązanie
Rozwiązanie YT
Rozwiązanie klasyczne
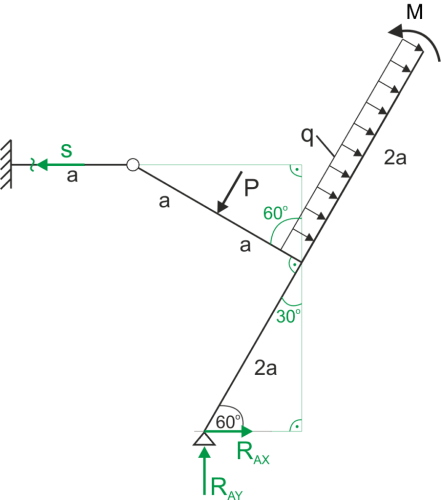 Siła w pręcie
\begin{aligned} &\sum{M_A}=0\\ &-Pa+2qa\cdot 3a-M-S(2a\cdot sin60+2a\cdot cos60)=0\\ &S=\frac{-Pa+2qa\cdot 3a-M}{(2a\cdot sin60+2a\cdot cos60)}\\ &S=\frac{-15\cdot 1 + 2\cdot 8\cdot 3 - 6}{2\cdot\frac{\sqrt 3}{2}+2\cdot\frac{1}{2}}=9,88 \ kN\\ &S=9,88 kN\\ \end{aligned}
Średnica z warunku wytrzymałościowego
\begin{aligned} &\sigma=|\frac{N}{A}|\le k_{r},k_{c}\\ &A=\frac{\pi d^{2}}{4}\\ &N=9,88\cdot 10^{3} \ N\\ &k_{r}=80 \ MPa\\ &\frac{9,88\cdot 10^{3}}{\frac{\pi d^{2}}{4}} \le 80\cdot 10^{6}\\ &\frac{9,88\cdot 10^{3}\cdot 4}{80\cdot 10^{6}\cdot\pi}\le d^{2}\\ &d\ge 0,0125 \ m\\ &d\ge 1,25 \ cm\\ \end{aligned}
Wydłużenie pręta
\begin{aligned}\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &A=\frac{\pi d^{2}}{4}\\ &d \ge 1,25 \ cm\\ &d=1,3 \ cm\\ &A=\frac{\pi(1,3\cdot 10^{-2})^{2}}{4}=1,33\cdot 10^{-4} \ m^{2}\\ &E=2\cdot 10^{5}\cdot 10^{6} Pa\\ &N=9,88\cdot 10^3 \ N\\ &\Delta l=\frac{9,88\cdot 10^{3}\cdot 1}{2\cdot 10^{11}\cdot 1,33\cdot 10^{-4}}=3,8\cdot 10^{-4} \ m=0,38 \ mm\\ \end{aligned}
Siła w pręcie
\begin{aligned} &\sum{M_A}=0\\ &-Pa+2qa\cdot 3a-M-S(2a\cdot sin60+2a\cdot cos60)=0\\ &S=\frac{-Pa+2qa\cdot 3a-M}{(2a\cdot sin60+2a\cdot cos60)}\\ &S=\frac{-15\cdot 1 + 2\cdot 8\cdot 3 - 6}{2\cdot\frac{\sqrt 3}{2}+2\cdot\frac{1}{2}}=9,88 \ kN\\ &S=9,88 kN\\ \end{aligned}
Średnica z warunku wytrzymałościowego
\begin{aligned} &\sigma=|\frac{N}{A}|\le k_{r},k_{c}\\ &A=\frac{\pi d^{2}}{4}\\ &N=9,88\cdot 10^{3} \ N\\ &k_{r}=80 \ MPa\\ &\frac{9,88\cdot 10^{3}}{\frac{\pi d^{2}}{4}} \le 80\cdot 10^{6}\\ &\frac{9,88\cdot 10^{3}\cdot 4}{80\cdot 10^{6}\cdot\pi}\le d^{2}\\ &d\ge 0,0125 \ m\\ &d\ge 1,25 \ cm\\ \end{aligned}
Wydłużenie pręta
\begin{aligned}\\ &\Delta l=\frac{N\cdot l}{E\cdot A}\\ &A=\frac{\pi d^{2}}{4}\\ &d \ge 1,25 \ cm\\ &d=1,3 \ cm\\ &A=\frac{\pi(1,3\cdot 10^{-2})^{2}}{4}=1,33\cdot 10^{-4} \ m^{2}\\ &E=2\cdot 10^{5}\cdot 10^{6} Pa\\ &N=9,88\cdot 10^3 \ N\\ &\Delta l=\frac{9,88\cdot 10^{3}\cdot 1}{2\cdot 10^{11}\cdot 1,33\cdot 10^{-4}}=3,8\cdot 10^{-4} \ m=0,38 \ mm\\ \end{aligned}
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: