Rozwiązanie
\begin{aligned}
&Q:=\left[\begin{array}{c}
0 \\
0 \\
2.5 \\
2 \\
0 \\
6 \\
0 \\
0
\end{array}\right] \cdot 10^{-2} \\
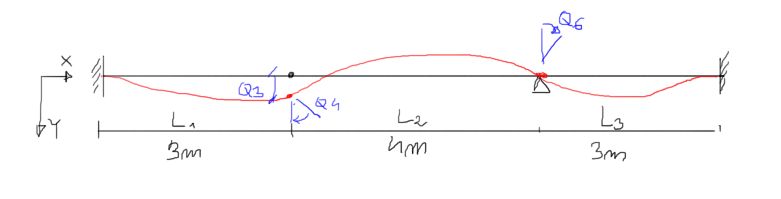
&L_{1}:=3 \quad m \\
&L_{2}:=4 \quad m \\
&L_{3}:=3 \quad m \\
&X:=9 \quad m \\
&\xi:=\frac{X-L_{1}-L_{2}}{L_{3}} \rightarrow \frac{2}{3} \\
&N_{1}:=1-3 \cdot \xi^{2}+2 \cdot \xi^{3}=0.259 \\
&N_{2}:=L_{3} \cdot\left(\xi-2 \cdot \xi^{2}+\xi^{3}\right)=0.222 \\
&N_{3}:=3 \cdot \xi^{2}-2 \cdot \xi^{3}=0.741 \\
&N_{4}:=L_{3} \cdot\left(\xi^{3}-\xi^{2}\right)=-0.444 \\
&v:=N_{1} \cdot q_{0}+N_{2} \cdot q_{1}+N_{3} \cdot q_{2}+N_{4} \cdot q_{3}=0.01333333 m
\end{aligned}
Jeżeli masz jakieś pytania, uwagi lub wydaje Ci się, że znalazłeś błąd w tym rozwiązaniu, napisz proszę do nas wiadomość na kontakt@edupanda.pl lub skontaktuj się z nami przez nasz profil na FB: