Zobacz wstęp teoretyczny do metody Maxwella-Mohra! W tym również nakierowanie na więcej zadań i materiałów z tego tematu!
Zobacz więcej na temat całkowania metodą Wereszczagina.

Rozwiązanie zadania:

W celu obliczenia szukanych przemieszczeń musimy narysować wykres momentów gnących od obciążenia zewnętrznego (początkowego).

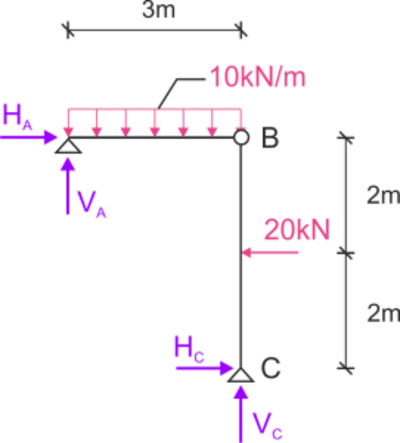
Wykres momentów od obciążenie zewnętrznego

\begin{aligned} \\ \sum&{{M_B^P}}=0 & &20\cdot 2-H_C\cdot 4=0 & &H_C;=10 kN\\ \sum&{X}=0 & &H_C;+H_A-20=0 & &H_A=10 kN\\ \sum&{M_C}=0 & &V_A\cdot 3-10\cdot3\cdot \frac{3}{2}=0 & &V_A=15 kN\\ \sum&{Y}=0 & &V_A+V_C-10\cdot 3=0 & &V_C=15 kN\\ \\ \end{aligned}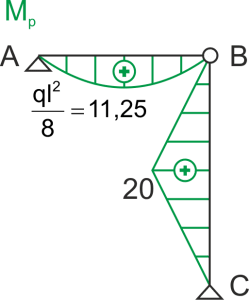

Zmiana kąta obrotu węzła B

W celu obliczenia zmiany kąta obrotu w węźle B (przegub) – przykładamy uogólnioną siłę odpowiadającą temu przemieszczeniu – czyli moment jednostkowy z jednej i drugiej strony przegubu (przeciwnie zwrócone). Szukane przemieszczenie to przecałkowany wykres momentów od obciążenia początkowego i wirtualnego na odpowiadających sobie prętach.

\begin{aligned} \\ =&\frac{1}{EJ}[\frac{2}{3}\cdot 11,25\cdot 3\cdot \frac{1}{2}+\frac{1}{6}\cdot 1\cdot 20\cdot 2 +\frac{1}{3}\cdot \frac{1}{2} \cdot 20\cdot 2+\frac{1}{3} \frac{1}{2} \cdot 20\cdot 2]=\\ =&\frac{31,25}{EJ}=2,345*10^{-3}[rad]*\frac{180}{\pi}=0,1343 ^{\circ}\\ \\ \end{aligned}

Kąt obrotu węzła A

Tym razem, jeżeli szukamy kąta obrotu węzła A, siłą uogólnioną odpowiadającą temu przemieszczeniu jest moment skupiony przyłożony w punkcie A.

\begin{aligned} \\ =&\frac{1}{EJ}[\frac{2}{3}\cdot 11,25\cdot \frac{1}{2}\cdot 3]=\frac{11,25}{EJ}=8,4427*10^{-4}[rad]*\frac{180}{\pi}=0,0484 ^{\circ}\\ \\ \end{aligned}