Zobacz wstęp teoretyczny do metody Maxwella-Mohra! W tym również nakierowanie na więcej zadań i materiałów z tego tematu!
Zobacz więcej na temat całkowania metodą Wereszczagina.

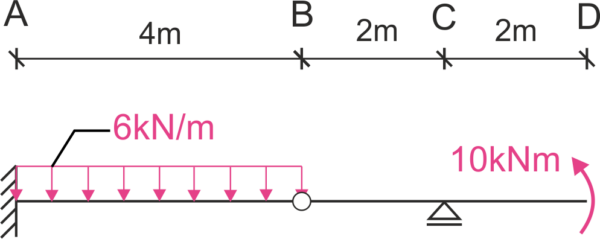
Rozwiązanie zadania:

Rozbijamy belkę przegubową na belki proste, liczymy reakcje bierne i rysujemy wykresy sił wewnętrznych.
Uwaga – reakcje można policzyć bez rozbijania na belki proste. Liczenie ekstremum nie jest potrzebne do policzenia przemieszczenia.

\begin{array}{l} \text { I } & \\ \sum M_{B}=0 & 10+2 V_{C}=0 \\ & V_{C}=-5 \mathrm{kN} \\ \sum Y=0 & V_{B}+V_{C}=0 \\ & V_{B}=5 \mathrm{kN} \end{array} \begin{array}{ll} \text { II } & \\ \sum M_{A}=0 & -M_{A}-6 \cdot 4 \cdot 2-4 V_{B}=0 \\ & M_{A}=-68 \mathrm{kNm} \\ \sum Y=0 & V_{A}-6 \cdot 4-V_{B}=0 \\ & V_{A}=29 \mathrm{kN} \end{array}

Stan jednostkowy

W celu obliczenia pionowego przemieszczenia w punkcie D przykładamy pionową siłę jednostkową i rysujemy wykresy sił wewnętrznych.

\begin{array}{l} \text { I} & \\ \sum M_{B}=0 & -1 \cdot 4+2 V_{C}=0 \\ & V_{C}=2 \\ \sum Y=0 & V_{B}+V_{C}-1=0 \\ & V_{B}=-1 \end{array} \begin{array}{ll} \text { II } & \\ \sum M_{A}=0 & -M_{A}-4 V_{B}=0 \\ & M_{A}=4 \\ \sum Y=0 & V_{A}-V_{B}=0 \\ & V_{A}=-1 \end{array}

Liczymy przemieszczenie uwzględniając wpływ momentu gnącego (dominujący) i siły tnącej. Jeżeli nie mamy danych liczbowych to zostawiamy wynik w takiej postaci jak poniżej.

\begin{aligned} \Delta_{D}=& \int \frac{M_{P} M_{1}}{E I} d x+\kappa \int \frac{Q_{P} Q_{1}}{G A}=\\ =& \frac{1}{E I}\left[-\frac{1}{3} \cdot 4 \cdot 68 \cdot 4+\frac{1}{3} \cdot 4 \cdot 4 \cdot \frac{6 \cdot 4^{2}}{8}-\frac{1}{3} \cdot 2 \cdot 2 \cdot 10-\frac{1}{2} \cdot 2 \cdot 2 \cdot 10\right]+\\ &+\frac{\kappa}{G A}\left[-\frac{1}{2} \cdot 4 \cdot 29 \cdot 1-\frac{1}{2} \cdot 4 \cdot 5 \cdot 1-2 \cdot 1 \cdot 5\right]=\\ =&-332 \frac{1}{E I}-78 \frac{\kappa}{G A} \end{aligned}

Żeby sobie uzmysłownić jak (najczęściej) dominujacy wpływ na ugiẹcie maja momenty zginające zobaczmy jakby wyglądały wyniki dla przykładowych danych liczbowych:

\(\mathrm{E}=210 \mathrm{GPa} \quad-\) moduł Younga
\(\mathrm{G}=80 \mathrm{GPa} \quad\) - moduł Kirchhoffa
Przekrój prostokątny \(10 \times 30 \mathrm{~cm}\)
\(\kappa=1.2 \quad\) - współczynnik dla ścinania
A \(=300 \mathrm{~cm}^2 \quad\) - pole przekroju poprzecznego
\(I=\frac{10 \cdot 30^3}{12}=22500 \quad \mathrm{~cm}^4 \quad\) - moment bezwładności na zginanie

Sztywność na zginanie i ścinanie

EI \(=210 \cdot 10^6 \cdot 22500 \cdot 10^{-8}=47250 \mathrm{kNm}^2 \quad\) - sztywność na zginanie
GA \(=80 \cdot 10^6 \cdot 300 \cdot 10^{-4}=2400000 \mathrm{kN} \quad\) - sztywność na ścinanie

Przemieszczenie po podstawieniu danych

\begin{aligned} & \Delta_{\mathrm{D}}=-332 \cdot \frac{1}{47250}-78 \cdot \frac{1.2}{2400000}=-7.026 \times 10^{-3} \mathrm{~m}-3.9 \times 10^{-5} \mathrm{~m}= \\ & \quad=-7.026 \mathrm{~mm}-0.039 \mathrm{~mm}=-7.065 \mathrm{~mm} \end{aligned}