Solution
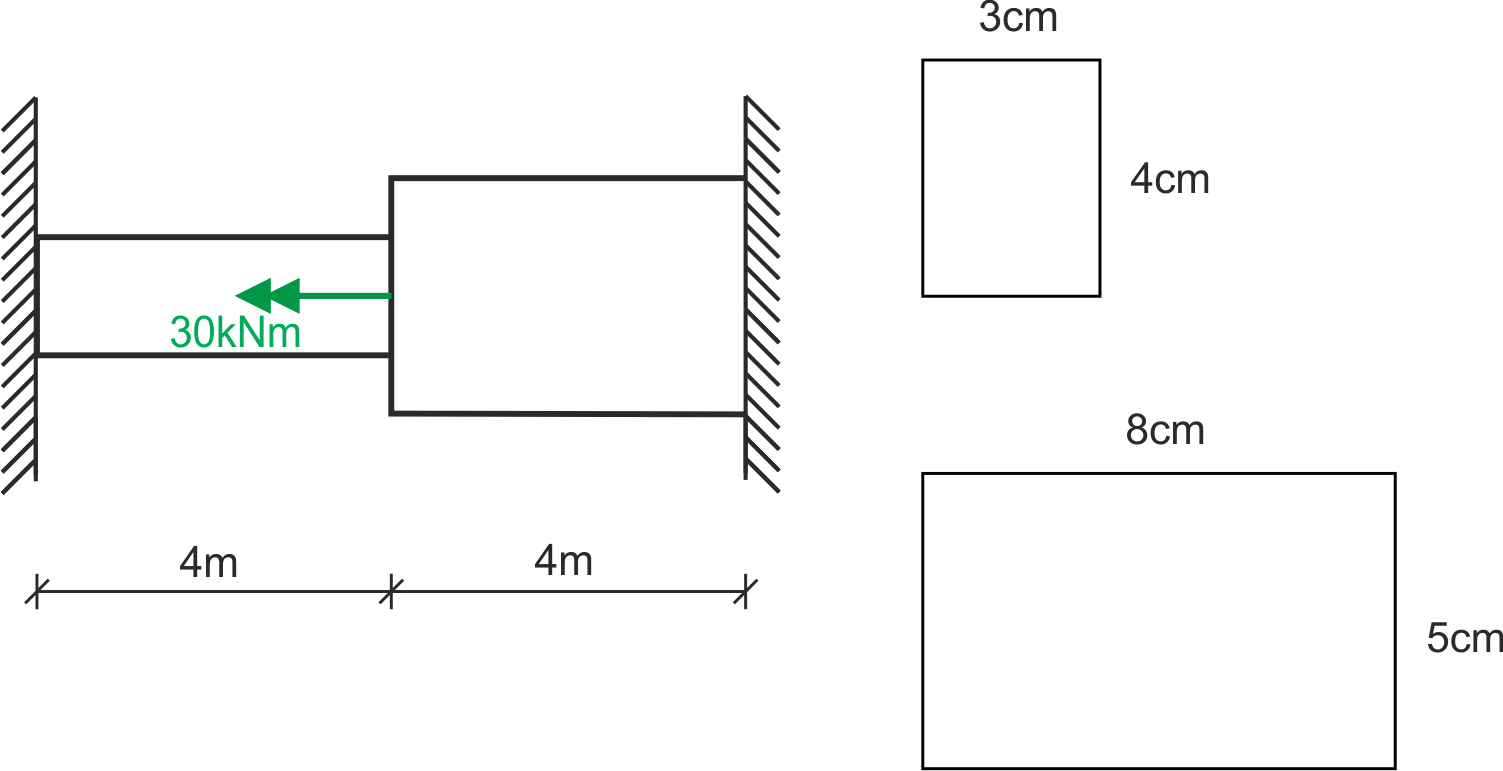
Les coefficients \(\alpha\) et \(\beta\) présents dans les formules pour le moment d'inertie et l'indice de résistance à la torsion sont donnés dans le tableau ci-dessous (ils dépendent du rapport h/b, où b est le côté plus court):
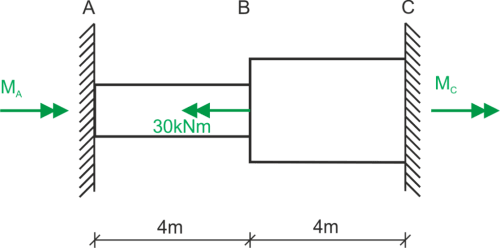
 \begin{aligned}\\ &M_{BC}=M_C\\ &M_{AB}=M_C-30\\ \end{aligned}
\begin{aligned}\\ &M_{BC}=M_C\\ &M_{AB}=M_C-30\\ \end{aligned}
Si les coefficients pour h/b recherché ne sont pas présents dans le tableau, nous devons interpoler les valeurs à partir des données adjacentes.
Partie AB
\begin{aligned}\\ &h/b=4/3\\ &\alpha (1,2)=0,219\\ &\alpha (1,4)=0,228\\ \end{aligned}Interpolation linéaire:
\begin{aligned}\\ &\alpha (1,33)=0,219+\frac{0,228-0,219}{0,2}\cdot 0,13=0,22485\\ &\beta (1,2)=0,166\\ &\beta (1,4)=0,187\\ &\beta (1,33)=0,166+\frac{0,187-0,166}{0,2}\cdot 0,13=0,17965\\ \end{aligned}Partie BC
\begin{aligned}\\ &h/b=8/5=1,6\\ &\alpha (1,6)=0,234\\ &\beta (1,6)=0,204\\ \end{aligned}Moment d'inertie à la torsion pour une section rectangulaire
\begin{aligned}\\ &I=\beta b^3 h\\ &I_{AB}=0,17965\cdot 0,03^3\cdot 0,04=1,94\cdot 10^{-7}\ m^4\\ &I_{BC}=0,204\cdot 0,05^3\cdot 0,08=2,04\cdot 10^{-6}\ m^4\\ \end{aligned}Pour faciliter les calculs ultérieurs, je détermine le rapport \( \frac{I_{BC}}{I_{AB}}\)
\begin{aligned}\\ &\frac{I_{BC}}{I_{AB}}=\frac{2,04\cdot 10^{-6}}{1,94\cdot 10^{-7}}=10,515\ \Rightarrow I_{BC}=10,515I_{AB}\\ \end{aligned}Condition géométrique - l'angle de torsion total est égal à 0: \(\varphi_c =0\)
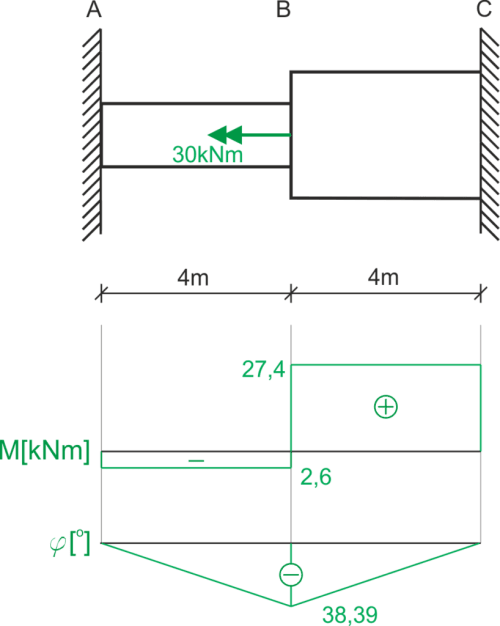
\begin{aligned}\\ &\varphi=\frac{M_S\cdot l}{G\cdot I}\\ \\ &\varphi_c=\varphi_{AB}+\varphi_{BC}=0\\ &\varphi_c=\frac{(M_C-30)\cdot 4}{G\cdot I_{AB}}+\frac{M_C\cdot 4}{G\cdot 10,515I_{AB}}=0\ |\cdot GI_{AB} :4\\ &M_C-30+0,095M_C=0\\ &1,095M_C=30\\ &M_C=27,4\ kNm\\ \end{aligned}Condition d'équilibre statique
\begin{aligned}\\ &\sum M=0\\ &M_A-30+M_C=0\\ &M_A=2,6\ kNm\\ \end{aligned}Contraintes de cisaillement
\begin{aligned}\\ &\tau =\frac{M_S}{W_S}\\ \end{aligned}Indice de résistance à la torsion pour une section rectangulaire
\begin{aligned}\\ &W_S=\alpha b^2 h\\ \\ &W_{S_{AB}}=0,22485\cdot 0,03^2\cdot 0,04=8,09\cdot 10^{-6}\ m^3\\ &W_{S_{BC}}=0,234\cdot 0,05^2\cdot 0,08=4,68\cdot 10^{-5}\ m^3\\ \\ &\tau_{AB}=\frac{M_{AB}}{W_{S_{AB}}}=\frac{-2,6\cdot 10^3}{8,09\cdot 10^{-6}}=-321,38\ MPa\\ \\ &\tau_{BC}=\frac{27,4\cdot 10^3}{4,68\cdot 10^{-5}}=585,47\ MPa\\ \end{aligned}Angle de torsion:
\begin{aligned}\\ &\varphi_A=\varphi_C=0\\ &\varphi_B=\varphi_A+\varphi_{AB}\\ &\varphi=\frac{M_S\cdot l}{G\cdot I}\\ &\varphi_B=\frac{-2,6\cdot 10^3\cdot 4}{80\cdot 10^9\cdot 1,94\cdot 10^{-7}}=-0,67\ rad=-38,39^o\\ \end{aligned}Graphiques