Solution
La figure a un axe de symétrie, nous prenons donc un des axes du repère dessus. Nous pouvons prendre n'importe quel autre axe, par exemple le long du bord inférieur comme indiqué ci-dessous.
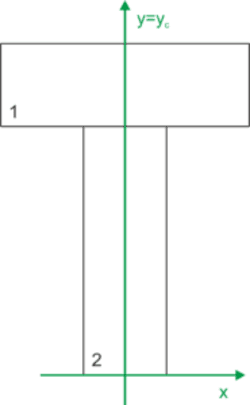
Nous recherchons la coordonnée verticale du centre de gravité "yc". Nous pouvons la calculer comme le quotient du moment d'inertie statique et de l'aire totale de la section. Il est utile d'écrire les coordonnées "y" et les aires des centres de gravité individuels des figures simples (y1 et y2) ainsi que leurs aires (A1 et A2).
Calcul de la position du centre de gravité
\begin{aligned} &y_1=3,5a & A_1=3a^2\\ &y_2=1,5a & A_2=3a^2\\ &y_c=\frac{y_1A_1+y_2A_2}{A_1+A_2}=\frac{3,5a\cdot 3a^2+1,5a\cdot 3a^2}{3a^2+3a^2}=2,5a\\ \end{aligned}Nous marquons le centre de gravité calculé sur le dessin et l'axe horizontal transféré au centre de gravité est l'axe central principal.
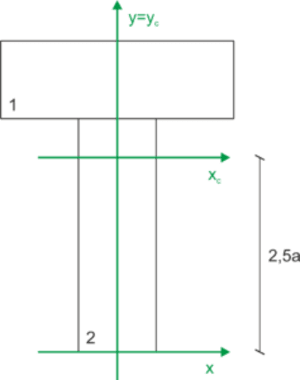
Calcul du moment d'inertie par rapport aux axes centraux principaux
Pour calculer le moment d'inertie par rapport à l'axe horizontal, nous devons utiliser le théorème de Steiners, ce qui n'est pas nécessaire pour l'axe vertical.
\begin{aligned} &I_{XC}=I_{X1}+A_1(y_1-y_C)^2+I_{X2}+A_2(y_2-y_C)^2\\ &I_{XC}=\frac{3a\cdot a^3}{12}+3a^2(3,5a-2,5a)^2+\frac{a\cdot(3a)^3}{12}+3a^2(1,5a-2,5a)^2=8,5a^4\\ &I_{YC}=I_{Y1}+I_{Y2}\\ &I_{YC}=\frac{(3a)^3\cdot a}{12}+\frac{a^3\cdot 3a}{12}=2,5a^4\\ \end{aligned}