Solution
Forces transverses
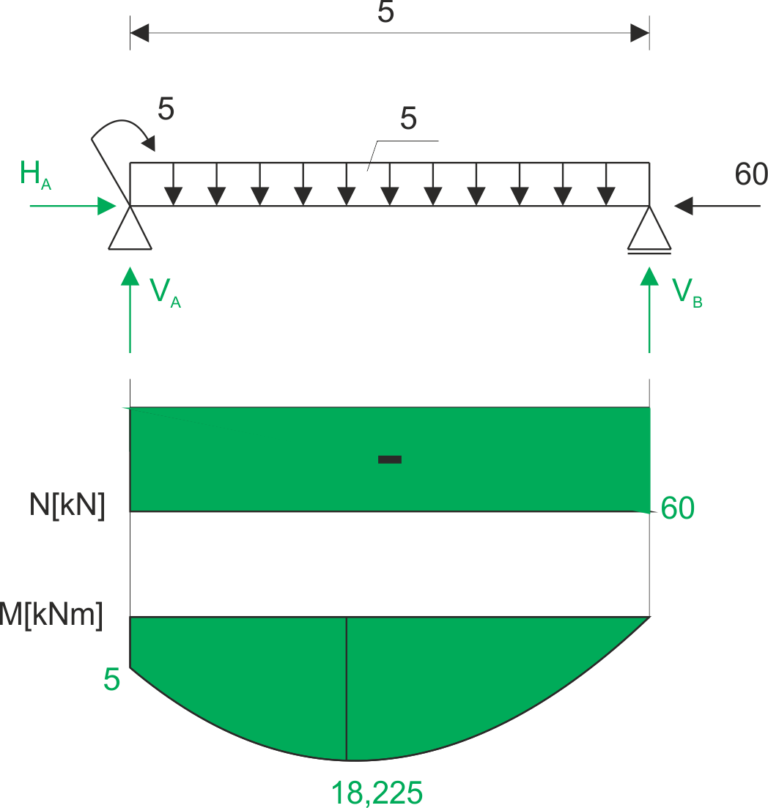
\begin{aligned} &\sum x=0 \\ &H_{A}=60 kN \\ &\sum M_{A}=5+5 \cdot 5 \cdot 2,5-V_{B} \cdot 5=0 \\ &V_{B}=13,5 kN \\ &\sum y=0 \\ &V_{A}-5 \cdot 5+13,5=0 \\ &V_{A}=11,5 kN \end{aligned}La fonction moment fléchissant :
\begin{aligned} M(x)=5+11,5 x-\frac{1}{2} \cdot 5 \cdot x^{2} \end{aligned}Je vérifie si elle est extrême :
\begin{aligned} &\frac{d M(x)}{d x}=11,5-5 x \\ &11,5-5 x=0 \Rightarrow x=2,3 \\ &M(0)=5 kNm \\ &M(5)=0 kNm \\ &M_{\text {extr }}(2,3)=5+11,5 \cdot 2,3-2,5 \cdot 2,3^{2}=18,225 kNm \end{aligned}Graphique de la force normale et du moment fléchissant
Contraintes normales
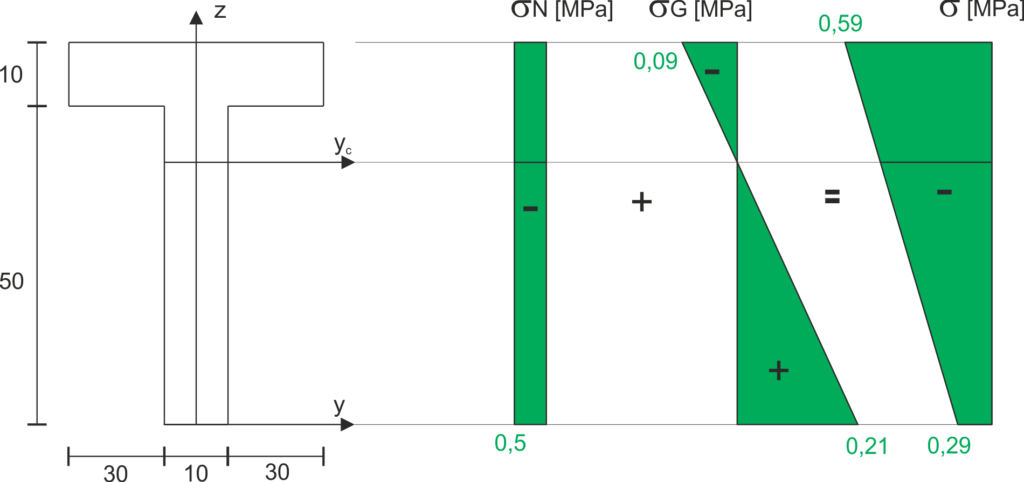
\begin{aligned} &\sigma_{N}=\frac{N}{A} \\ &A=10 \cdot 50+10 \cdot 70=1200 \mathrm{~cm}^{2} \\ &\sigma_{N}=\frac{-60 \cdot 10^{3}}{1200 \cdot 10^{-4}}=-0,5 \mathrm{MPa} \\ &\sigma_{G}=\frac{M_{y}}{I_{y}} z \end{aligned}Caractéristiques géométriques
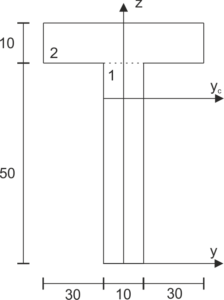 \begin{aligned}
z_{1} &=25 \mathrm{~mm} \\
z_{2} &=55 \mathrm{~mm} \\
A_{1} &=500 \mathrm{~mm}^{2} \\
A_{2} &=700 \mathrm{~mm}^{2} \\
z_{c} &=\frac{z_{1} \cdot A_{1}+z_{2} \cdot A_{2}}{A_{1}+A_{2}}=42,5 \mathrm{~mm} \\
I_{y c} &=\frac{10 \cdot 50^{3}}{12}+500 \cdot(25-42,5)^{2}+\frac{70 \cdot 10^{3}}{12}+700 \cdot(55-42,5)^{2}=372500 \mathrm{~cm}^{4} \\
\sigma_{G}^{d} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot 0,0425=0,21 \mathrm{MPa} \\
\sigma_{G}^{g} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot(0,06-0,0425)=-0,09 \mathrm{MPa}
\end{aligned}
Le graphique final des contraintes normales est obtenu en ajoutant, aux points caractéristiques (fibres inférieures et supérieures), des contraintes de compression et de flexion
\begin{aligned}
z_{1} &=25 \mathrm{~mm} \\
z_{2} &=55 \mathrm{~mm} \\
A_{1} &=500 \mathrm{~mm}^{2} \\
A_{2} &=700 \mathrm{~mm}^{2} \\
z_{c} &=\frac{z_{1} \cdot A_{1}+z_{2} \cdot A_{2}}{A_{1}+A_{2}}=42,5 \mathrm{~mm} \\
I_{y c} &=\frac{10 \cdot 50^{3}}{12}+500 \cdot(25-42,5)^{2}+\frac{70 \cdot 10^{3}}{12}+700 \cdot(55-42,5)^{2}=372500 \mathrm{~cm}^{4} \\
\sigma_{G}^{d} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot 0,0425=0,21 \mathrm{MPa} \\
\sigma_{G}^{g} &=\frac{18,225 \cdot 10^{3}}{372500 \cdot 10^{-8}} \cdot(0,06-0,0425)=-0,09 \mathrm{MPa}
\end{aligned}
Le graphique final des contraintes normales est obtenu en ajoutant, aux points caractéristiques (fibres inférieures et supérieures), des contraintes de compression et de flexion
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.
