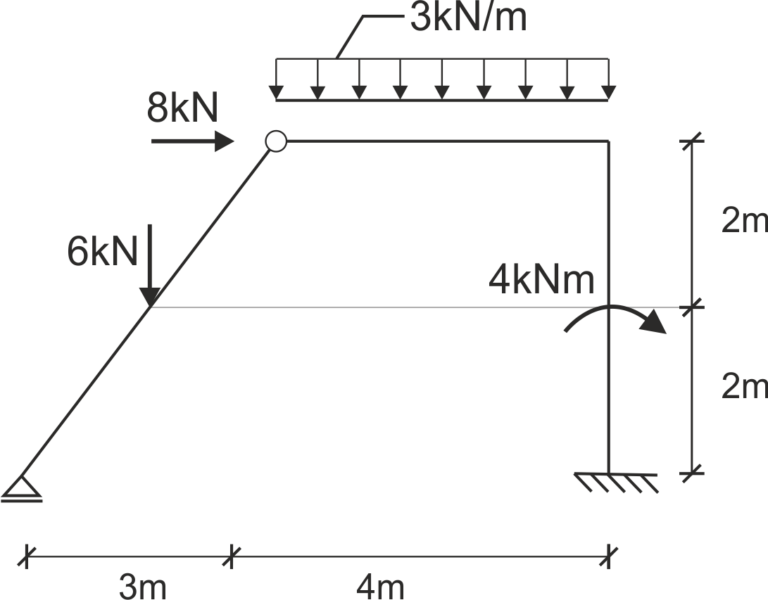
Solution

Réactions
\begin{aligned} &\sum M_{C . l}=0\\ &-6 \cdot \frac{3}{2}+V_{A} \cdot 3=0\\ &V_{A}:=\frac{6 \cdot \frac{3}{2}}{3}=3\\ &\Sigma X=0\\ &8-H_{F}=0\\ &H_{F}:=8\\ &\Sigma Y=0\\ &V_{A}-6-3 \cdot 4+V_{F}=0\\ &V_{F}:=-\left(V_{A}-6-3 \cdot 4\right)=15\\ &\Sigma M_{A}=0\\ &6 \cdot \frac{3}{2}+8 \cdot 4+3 \cdot 4 \cdot 5+4-V_{F} \cdot 7+M_{F}=0\\ &M_{F}:=-\left(6 \cdot \frac{3}{2}+8 \cdot 4+3 \cdot 4 \cdot 5+4-V_{F} \cdot 7\right)=0 \end{aligned}Intervalle AB \( 0 \leq x \leq 1.5\)

\begin{aligned}
&Q_{A B}=3 \cos (\alpha)=1.8 \quad k N \\
&M_{A B}(x):=3 x \\
&M_{A B}(0)=0 \\
&M_{A B}(1.5)=4.5 \quad k N m \\
&N_{A B}=3 \sin (\alpha)=-2.4 \quad k N
\end{aligned}
Intervalle BC \( 1.5 \leq x \leq 3\)

\begin{aligned}
&Q_{A B}=3 \cos (\alpha)-6 \cos (\alpha)=-1.8 \mathrm{kN} \\
&M_{A B}(x):=3 x-6 \cdot(x-1.5) \\
&M_{A B}(1.5)=4.5 \quad k N m \\
&M_{A B}(3)=0 \\
&N_{A B}=3 \sin (\alpha)+6 \sin (\alpha)=-2.4 \quad k N
\end{aligned}
Graphiques



Équilibre du nœud C

\begin{aligned}
&\Sigma X=0\\
&8-8-2.4 \cdot \cos (\alpha)+1.8 \cdot \sin (\alpha)=0\\
&L=P\\
&\Sigma Y=0\\
&3-2.4 \cdot \sin (\alpha)+1.8 \cdot \cos (\alpha)=0\\
&L=P
\end{aligned}
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.