Solution
Nous vous encourageons à regarder la solution de cet exemple (et d'autres) sur notre chaîne YouTube. Nous expliquons étape par étape comment résoudre cet exercice. Regarder cette vidéo vous aidera également à comprendre d'autres exemples sur notre site.
\begin{aligned}\\ &Q(x)=-30+15x\\ &Q(x=0)=-30\ kN\\ &Q(x=6)=60\ kN\\ &Extremum \\ &Q(x)=-30+15x=0\\ &x=2[m]\\ &M(x=0)=30\cdot 6-\frac{1}{2}\cdot 15\cdot 6^2=-90\ kNm\\ &M_{max}(x-2)=30\ kNm\\ &M(x=6)=30\cdot 6-\frac{1}{2}\cdot 15\cdot 6^2=-90\ kNm\\ \end{aligned}Diagramme des forces transverses et des moments fléchissants
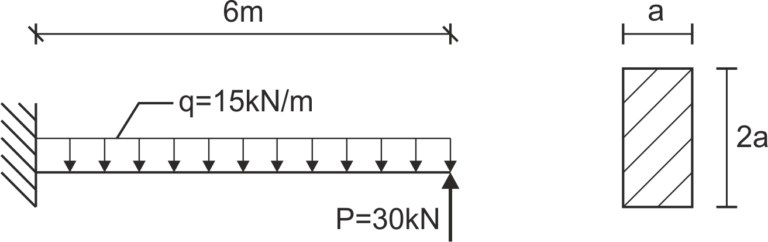
Dimensionnement
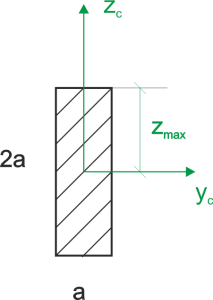 \begin{aligned}\\ &I_{y_c}=\frac{b*h^3}{12}=\frac{a*(2a)^3}{12}=\frac{2}{3}a^4 \\ &W=\frac{I_{y_c}}{z_{max}}=\frac{\frac{2}{3}a^4}{a}=\frac{2}{3}a^3\\ \end{aligned}
\begin{aligned}\\ &I_{y_c}=\frac{b*h^3}{12}=\frac{a*(2a)^3}{12}=\frac{2}{3}a^4 \\ &W=\frac{I_{y_c}}{z_{max}}=\frac{\frac{2}{3}a^4}{a}=\frac{2}{3}a^3\\ \end{aligned}
Condition de résistance
\begin{aligned}\\ &|\frac{M_{max}}{W}|\le k_g\\ &\frac{90*10^3}{\frac{2}{3}a^3}\le 160*10^6\\ &a\ge 0,09449 \ m\\ & a=95\ mm\\ \end{aligned}Contraintes
\begin{aligned}\\ &\sigma=\frac{M}{W}=\frac{90*10^3}{\frac{2}{3}*(0,095)^3}=157,46 \ MPa\\ \end{aligned}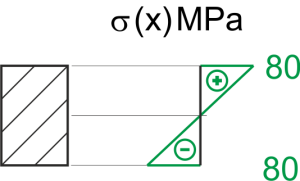
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.
