Avant de commencer cet exemple, nous vous encourageons à lire une brève introduction théorique sur la page précédente.

Nous calculons les réactions d'appui et traçons le diagramme des moments. Ensuite, nous convertissons la poutre réelle en une poutre fictive et la chargeons correctement.

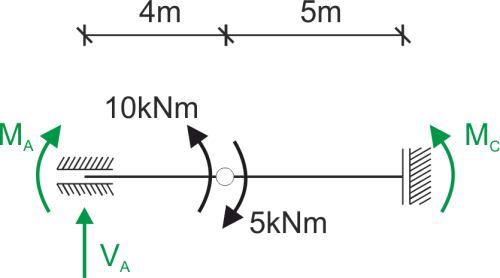\begin{aligned} &\sum M_B^P=0\\ &5-M_C=0\ \Rightarrow M_C=5\ kNm\\ &\sum M_B^L=0\\ &M_A-10=0\ \Rightarrow M_A=10\ kNm\\ &\sum y=0\\ &V_A=0\\ \end{aligned}

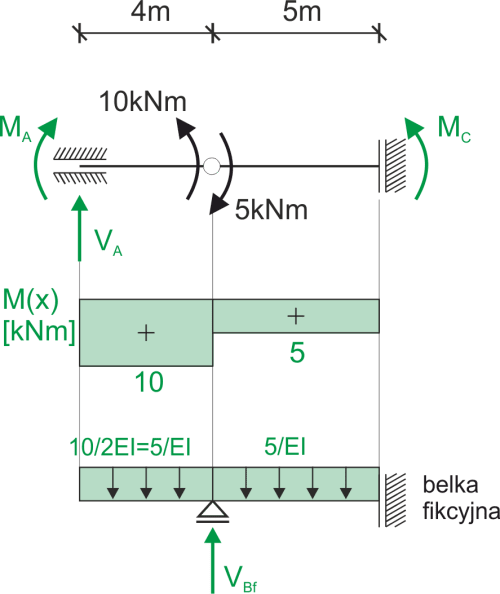
Poutre fictive

\begin{aligned} &\sum y=0\\ &V_{Bf}-\frac{5}{EI}\cdot 9=0\\ &V_{Bf}=\frac{45}{EI}\\ \\ &w_B=M_{fB}=-\frac{5}{EI}\cdot 4\cdot 2=-\frac{40}{EI}\\ &w_C=M_{fC}=-\frac{5}{EI}\cdot 9\cdot 4,5+\frac{45}{EI}\cdot 5=\frac{22,5}{EI}\\ \end{aligned}

Caractéristiques de la section, rigidité à la flexion EI

\begin{aligned} &E=200 GPa\\ &I=\frac{0,15\cdot 0,2^3}{12}=1\cdot 10^{-4}\ m^4\\ &EI=(200\cdot 10^9\cdot 1\cdot 10^{-4})\cdot 10^{-3}=20 000\ kNm^2\\ \end{aligned}

Calcul des déplacements recherchés

\begin{aligned} &w_B=-\frac{40}{20 000}=-2\ mm\\ &w_C=\frac{22,5}{20000}=1,125\ mm\\ \end{aligned}