Solution
1. Détermination du degré de non-déterminabilité cinématique :
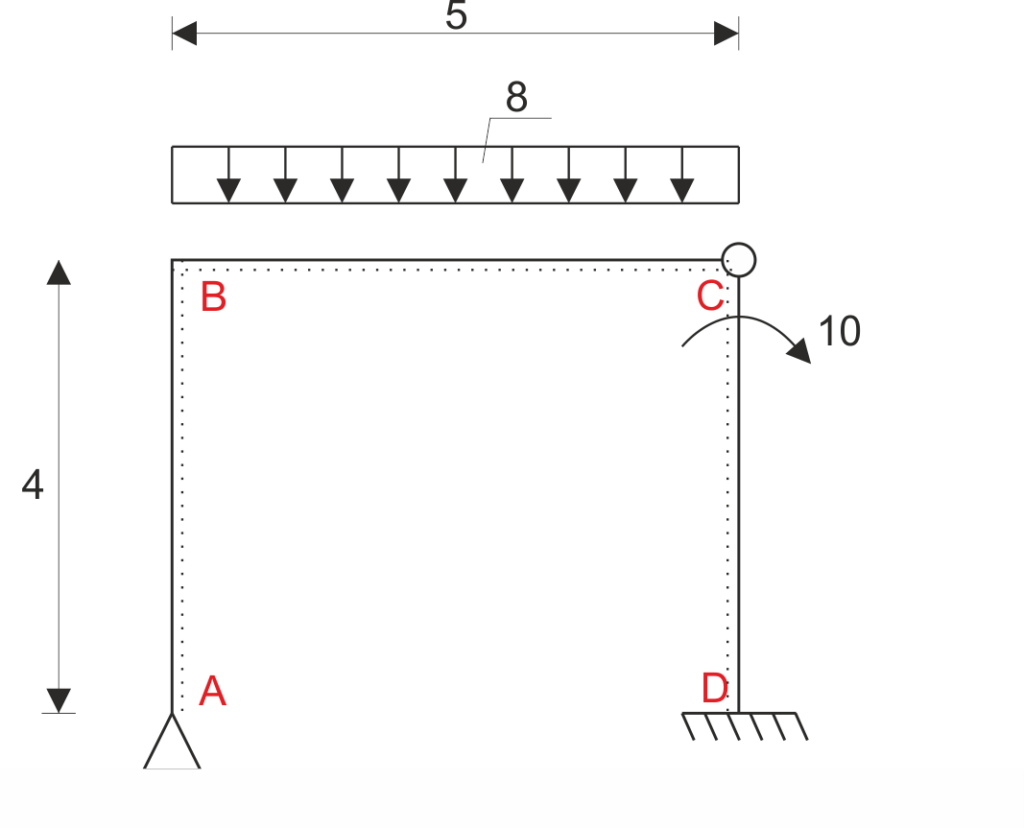
| \begin{aligned} &SKN=\sum \varphi +\sum \Delta\\ &SKN=1+1=2\\ \end{aligned} |
2. Sélection du système de base de la méthode des déplacements (UPMP) :
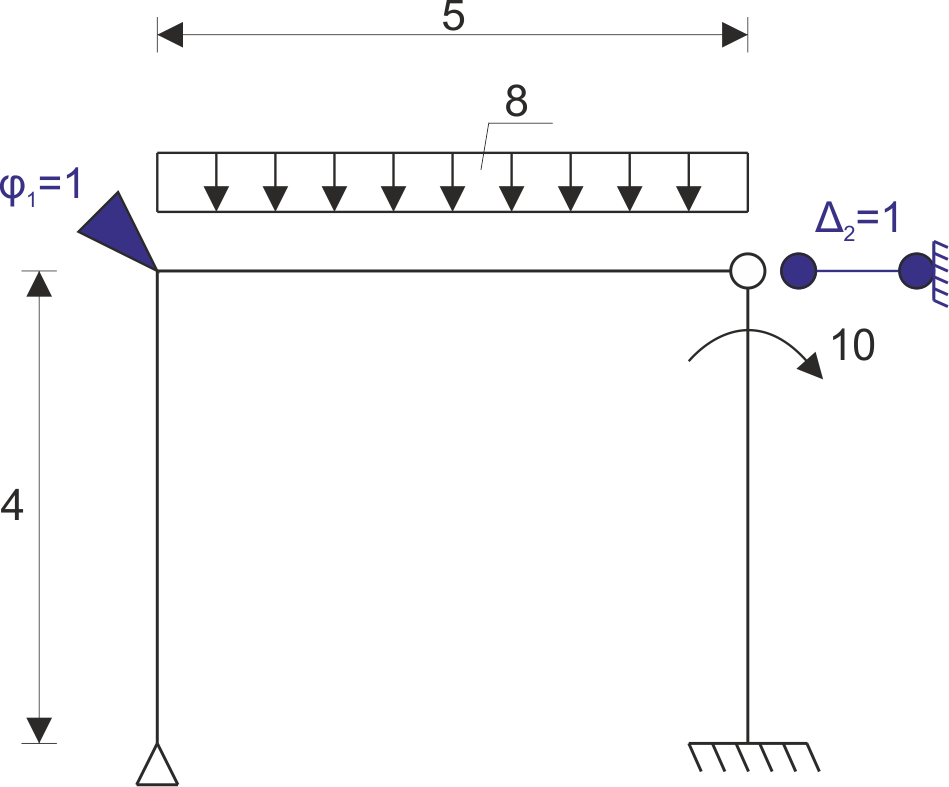
Système d'équations canoniques de la méthode des déplacements:
\( r_{11}\cdot\varphi_{1} +r_{12}\cdot\Delta_{2}+r_{1p}=0\\ r_{21}\cdot\varphi_{1} +r_{22}\cdot\Delta_{2}+r_{2p}=0\\ \)
3. Graphiques et détermination des coefficients et termes indépendants des équations :
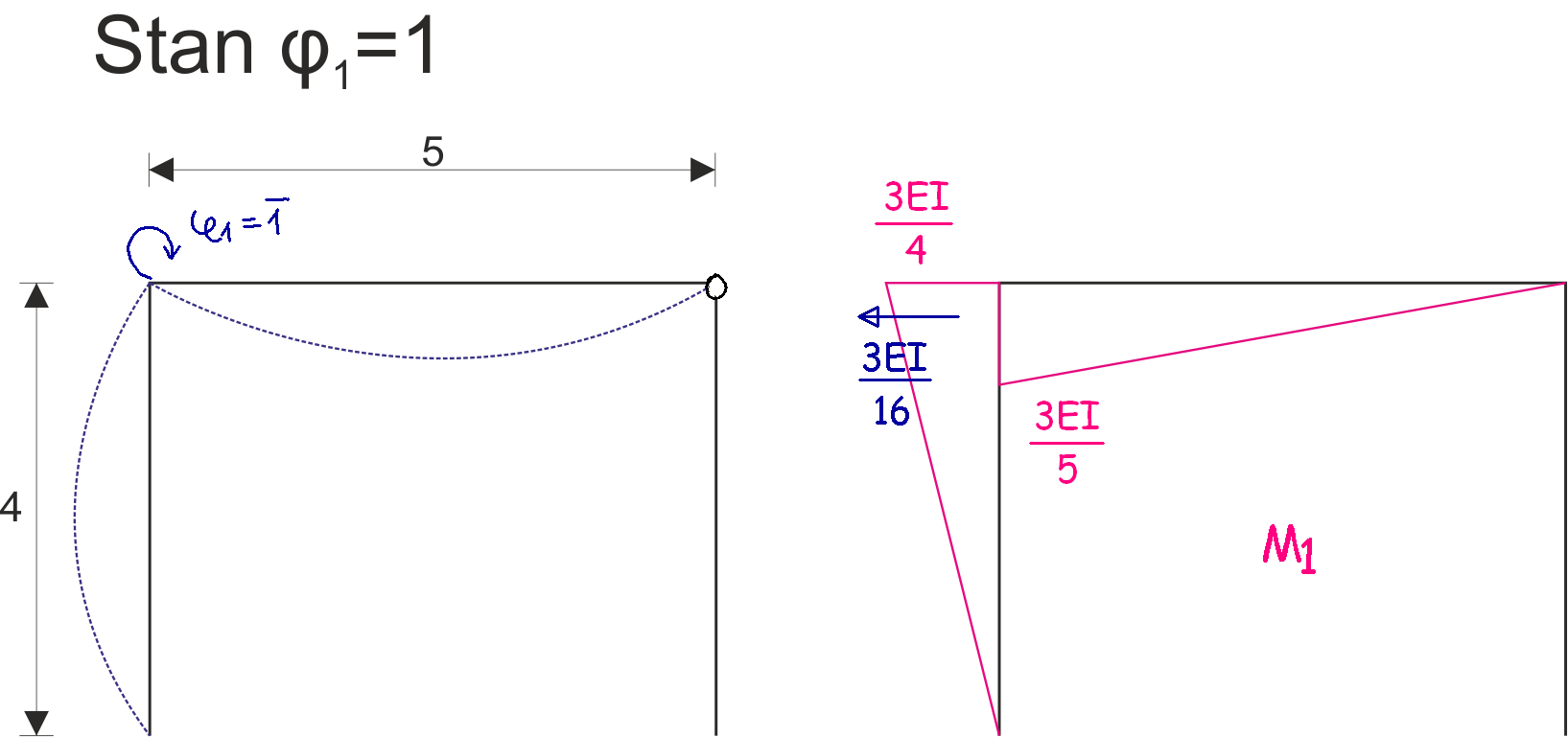
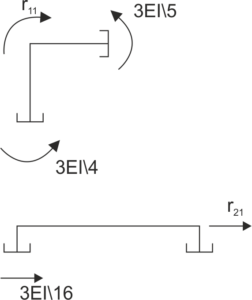
Détermination des coefficients UPMP
|
\begin{aligned} &r_{11}=\frac{3EI}{5}+\frac{3EI}{4}=\frac{27EI}{20}\\ \\ \\ &r_{21}=-\frac{3EI}{16}\\ \end{aligned} |
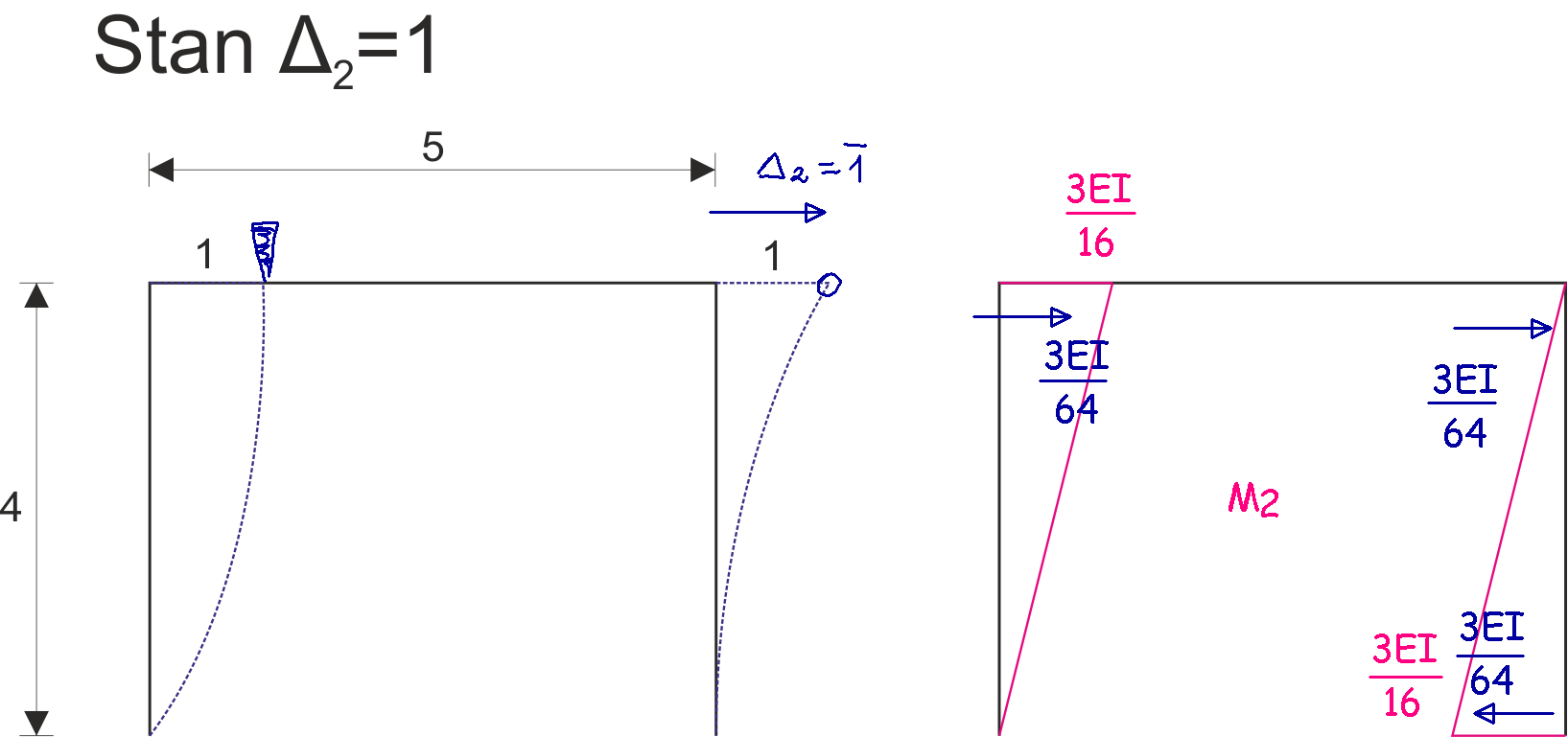
Détermination des coefficients UPMP

|
\begin{aligned} &r_{12}=-\frac{3EI}{16}\\ \\ \\ &r_{22}=\frac{3EI}{32}\\ \end{aligned} |
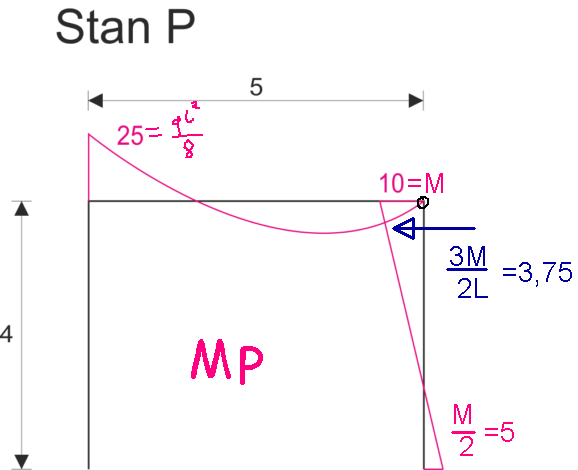
|
Détermination des coefficients UPMP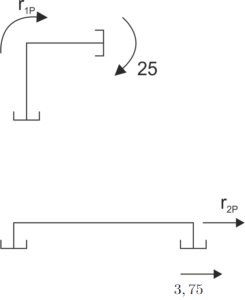
|
\begin{aligned} &r_{1p}=-25\\ \\ \\ \\ &r_{2p}=-3,75\\ \end{aligned} |
4. Résolution du système d'équations canoniques :
\begin{aligned} &\frac{27EI}{20}\cdot\varphi_{1} -\frac{3EI}{16}\cdot\Delta_{2}=25\\ &-\frac{3EI}{16}\cdot\varphi_{1} +\frac{3EI}{32}\cdot\Delta_{2}=3,75\\ \\ &\varphi_{1} =33,33/EI\\ &\Delta_{2}=106,67/EI\\ \end{aligned}5. Graphiques finaux des forces de section dans la poutre :
Graphique des moments [kNm]\( M_{ost}=M_{p}+M_{1} \cdot \varphi_{1}+M_{2} \cdot \Delta_{2}\\ \)
| \begin{aligned} & \mathrm{M}_{\mathrm{A}}=0 \cdot \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{BA}}=\frac{-3 \mathrm{EI}}{4} \cdot \varphi_1+\frac{3 \mathrm{EI}}{16} \cdot \Delta_2=-5 \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{BC}}=\frac{3 \mathrm{EI}}{5} \varphi_1-25=-5 \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{CB}}=0 \cdot \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{CD}}=10 \cdot \mathrm{kNm} \\ & \mathrm{M}_{\mathrm{D}}=\frac{3 \mathrm{EI}}{16} \cdot \Delta_2-5=15 \mathrm{kNm} \end{aligned} |
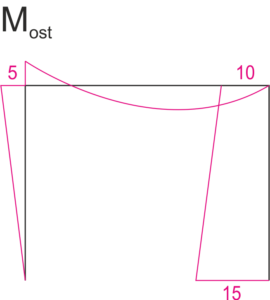
|
Calculs pour le graphique des forces tranchantes
Element BC: 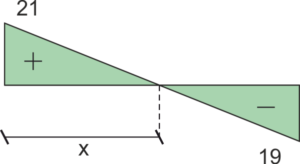 |
\begin{aligned}
&\sum{M_{C}}=0\\
&{Q_{BC}}\cdot 5-5-8\cdot 5\cdot 2,5=0\\
&{Q_{BC}}=21 \ kN\\
&\sum{Y}=0\\
&-{Q_{CB}}+21-40=0\\
&{Q_{CB}}=-19 \ kN\\
\end{aligned}
à l'élément BC: |
|
Élément AB: 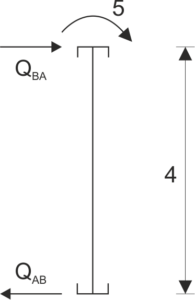
| \begin{aligned} &\sum{M_{A}}=0\\ &{Q_{BA}}\cdot 4+5=0\\ &{Q_{BA}}=-1,25 \ kN\\ &{Q_{AB}}=-1,25\\ \end{aligned} |
Élément CD: 
| \begin{aligned} &\sum{M_{D}}=0\\ &{Q_{CD}}\cdot 4+10-15=0\\ &{Q_{CD}}=1,25 \ kN\\ &{Q_{DC}}=1,25 \ kN\\ \end{aligned} |
Graphiques finaux des forces normales [kN]
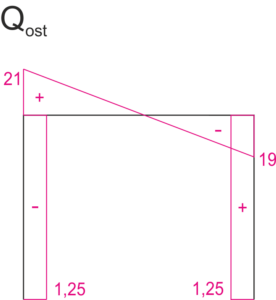
Calculs pour le graphique des forces longitudinales
|
nœud B 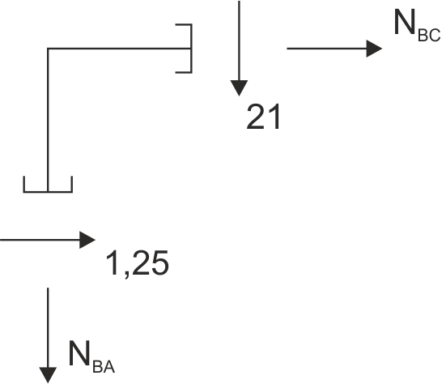 \begin{aligned}
&\sum{X}=0\\
&N_{BC}=-1,25 \ kN\\
&\sum{Y}=0\\
&N_{BA}=-21 \ kN\\
\end{aligned}
\begin{aligned}
&\sum{X}=0\\
&N_{BC}=-1,25 \ kN\\
&\sum{Y}=0\\
&N_{BA}=-21 \ kN\\
\end{aligned}
|
nœud C 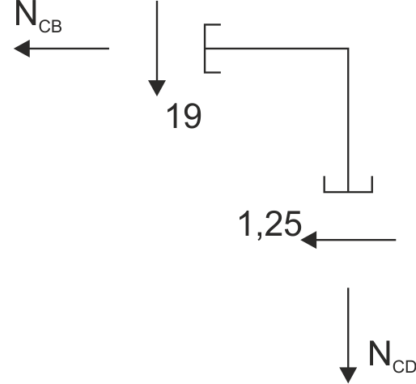 \begin{aligned}
&\sum{X}=0\\
&N_{CB}=-1,25 \ kN\\
&\sum{Y}=0\\
&N_{CD}=-19 \ kN\\
\end{aligned}
\begin{aligned}
&\sum{X}=0\\
&N_{CB}=-1,25 \ kN\\
&\sum{Y}=0\\
&N_{CD}=-19 \ kN\\
\end{aligned}
|
Graphiques des forces axiales [kN]

6. Vérification cinématique
Nous choisissons un système déterminable et traçons le graphique des moments en fonction de la force unitaire. (degré de non-déterminabilité statique SSN=1)
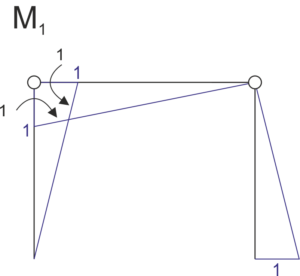 \begin{aligned}
&\delta_1 =\int \frac{M_{ost}\cdot M_{1}}{EJ} dx= \frac{1}{EI} \left( -\frac{1}{3}\cdot 1\cdot 5\cdot 4 -\frac{1}{3} \cdot 1\cdot 5\cdot 5 +\frac{1}{3} \frac{8\cdot 5^2}{8} \cdot 1 \cdot 5 -\frac{4}{6} \cdot (2\cdot 1\cdot 15 + 10)\right) \approx 0\\
\end{aligned}
\begin{aligned}
&\delta_1 =\int \frac{M_{ost}\cdot M_{1}}{EJ} dx= \frac{1}{EI} \left( -\frac{1}{3}\cdot 1\cdot 5\cdot 4 -\frac{1}{3} \cdot 1\cdot 5\cdot 5 +\frac{1}{3} \frac{8\cdot 5^2}{8} \cdot 1 \cdot 5 -\frac{4}{6} \cdot (2\cdot 1\cdot 15 + 10)\right) \approx 0\\
\end{aligned}
7. Vérification statique
Nous lisons les réactions (valeurs et sens corrects) à partir des graphiques des forces normales, tranchantes et des moments fléchissants.Ensuite, nous écrivons les équations d'équilibre statique et vérifions si toutes les équations sont satisfaites pour ces réactions lues.
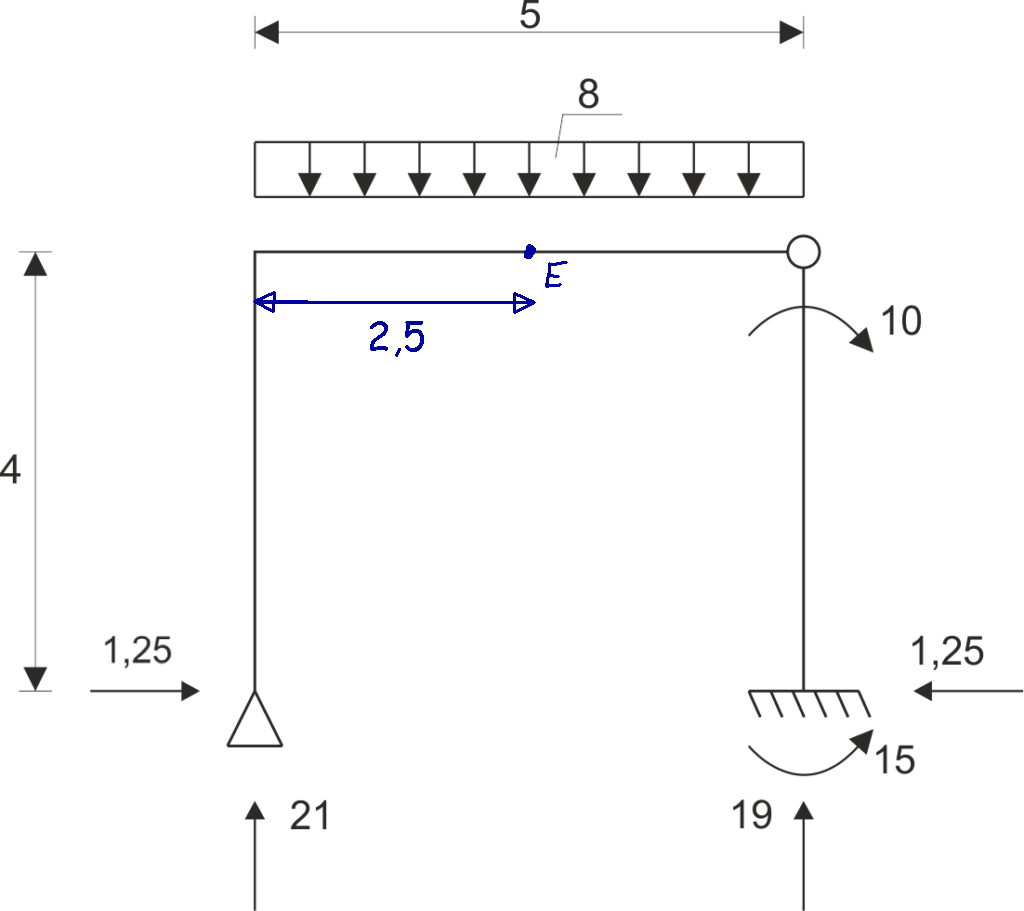
| \begin{aligned} &\sum{X}=0 \hspace{2cm} 1,25-1,25=0\\ &\sum{Y}=0 \hspace{2cm} 21+19-4\cdot8=0\\ &\sum{M_{E}}=0\hspace{1.65cm} 21\cdot 2,5-1,25\cdot 4+10-15+1,25\cdot 4-19\cdot 2,5=0\\ \end{aligned} |
Si vous avez des questions, des remarques ou si vous pensez avoir trouvé une erreur dans cette solution, veuillez nous envoyer un message à kontakt@edupanda.pl.
