Solution
Degré d'indéterminabilité statique
SSN=3-3=0Nombre de degrés de liberté dynamique
LSSD=1
\( m_1=m \)
Sur le point et dans la direction du degré de liberté dynamique, nous appliquons une force unitaire et traçons le graphique des moments dus à cette charge
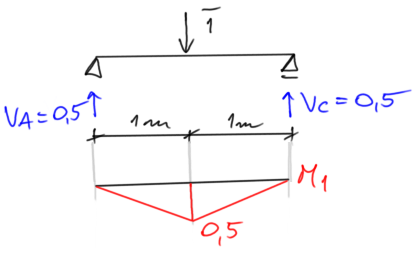
Delta dynamique $$ \delta_{11}:=\frac{1}{\mathrm{EI}} \cdot\left(\frac{1}{3} \cdot 0.5 \cdot 0.5 \cdot 1+\frac{1}{3} \cdot 0.5 \cdot 0.5 \cdot 1\right)=\frac{1}{6} \cdot \frac{1}{\mathrm{EI}} $$ Problème propre de la dynamique pour LSSD=1 $$ \left(\delta_{11} \cdot \mathrm{m}_1 \cdot \omega^2-1\right) \cdot \mathrm{A}=0 $$ En divisant des deux côtés par A et en transformant l'équation, nous obtenons \begin{aligned} &\omega_1 =\sqrt{\frac{1}{m_1 \cdot \delta_{11}}}\\ &\text{Rigidité à la flexion} \\ &EI=210\cdot 10^9 \cdot 10\cdot 10^{-8}=21 000 Nm^2 \\ &\text{Fréquence propre des vibrations: }\\ &\omega_1 =\sqrt{\frac{1}{10\cdot \frac{1}{6\cdot 21 000}}}=112,25\frac{rad}{s}\\ \\ \end{aligned}
Conversion de la fréquence d'excitation en unité de base (de Hz à rad/s), note - la fréquence d'excitation est parfois également indiquée par le symbole θ ou p.
\begin{aligned} &\text{Fréquence d'excitation: }\\ &\omega_w = 2\pi \cdot f_v=2\cdot \pi \cdot 5=31,42\frac{rad}{s}\\ \end{aligned}La résonance se produit lorsque la fréquence d'excitation est trop proche de la fréquence propre des vibrations, on suppose que la fréquence d'excitation ne peut pas être comprise entre 0,85ω et 1,15ω.
\( \omega_w/\omega_1=31,42/112,25=0,28 \)Pas de résonance.
Amplitude des vibrations forcées
\( \left(\delta_{11} \cdot m_1 \cdot \omega_w^2-1\right) \cdot A+\Delta_{1 p}=0 \)
Si la force d'excitation se trouve sur un degré de liberté dynamique, alors
\( \Delta_1p=\delta_{11}\cdot P \) \begin{aligned} &A=\frac{\delta_{11}\cdot P}{1-\omega_w^2 \cdot \delta_{11} \cdot m}\\ &A=\frac{\frac{1}{6\cdot 21 000}\cdot 100}{1-31,42^2 \cdot \frac{1}{6\cdot 21 000} \cdot 10}=8,61\cdot 10^{-4}m=0,86 mm\\ \\ &\text{Force d'inertie:}\\ &B=\frac{\delta_{11} \cdot P}{\frac{1}{\omega_w^2 \cdot m}-\delta_{11}}\\ &B=\frac{\frac{1}{6\cdot 21 000} \cdot 100}{\frac{1}{31,42^2 \cdot 10}-\frac{1}{6\cdot 21 000}}=8,5 N\\ \end{aligned}