Solución
Versión de YouTube
Versión clásica
Te animamos a ver la solución de este ejemplo (y otros) en nuestro canal de YouTube. Explico cómo resolver esta tarea paso a paso. Ver este video también te ayudará a comprender otros ejemplos en nuestro sitio web.
Condiciones geométricas: el ángulo total de torsión es igual a 0:
\begin{aligned}\\ &\varphi_c =0\\ &\varphi=\frac{M_S\cdot l}{G\cdot I}\\ \\ &M_{AB}=M_A\\ &M_{BC}=M_A-3M_0\\ &M_{CD}=M_A-4M_0\\ \\ &I=\frac{\pi \cdot d^4}{32}\\ \\ &I_{AB}=I_{BC}=\frac{\pi \cdot (2d)^4}{32}=\frac{\pi \cdot d^4}{2}\\ &I_{CD}=\frac{\pi \cdot d^4}{32}\\ \end{aligned}Para facilitar cálculos posteriores, determinamos la relación entre los momentos de inercia:
\begin{aligned}\\ &\frac{I_{AB}}{I_{CD}}=\frac{\pi d^4}{2}\cdot \frac{32}{\pi d^4}=16\ \Rightarrow I_{AB}=16I_{BC}\\ \\ &\varphi_c=\varphi_{AB}+\varphi_{BC}+\varphi_{CD}=0\\ &\varphi_c=\frac{M_A\cdot l}{G\cdot 16I_{CD}}+\frac{(M_A-3M_0)\cdot l}{G\cdot 16I_{CD}}+\frac{(M_A-4M_0)\cdot l}{G\cdot I_{CD}}=0\ |\cdot \frac{GI_{BC}}{l}\\ &\frac{1}{16}M_A+\frac{1}{16}M_A-\frac{3}{16}M_0+M_A-4M_0=0\\ &\frac{18}{16}M_A=\frac{67}{16}M_0\\ &M_A=\frac{67}{18}M_0=3,72M_0=3,72\ kNm\\ \end{aligned}Tensiones tangenciales
\begin{aligned}\\ &\tau =\frac{M_S}{W_S}\\ &W_S=\frac{\pi \cdot d^3}{16}\\ \\ &W_{S_{AB}}=W_{S_{BC}}=\frac{\pi \cdot 0,1^3}{16}=1,96\cdot 10^{-4}\ m^3\\ &W_{S_{CD}}=\frac{\pi \cdot 0,05^3}{16}=2,45\cdot 10^{-5}\ m^3\\ \\ &\tau_{AB}=\frac{M_{AB}}{W_{S_{AB}}}=\frac{3,72\cdot 10^3}{1,96\cdot 10^{-4}}=18,98\ MPa\\ \\ &\tau_{BC}=\frac{0,72\cdot 10^3}{2,45\cdot 10^{-5}}=3,67\ MPa\\ &\tau_{CD}=\frac{-0,28\cdot 10^3}{2,45\cdot 10^{-5}}=-11,43\ MPa\\ \end{aligned}Ángulo de torsión de la sección C
El ángulo de torsión entre dos secciones separadas por una distancia x es igual a:
\begin{aligned} &\varphi =\int\limits_{0}^{x} \frac{M_s(x)}{GI_0}dx\\ \end{aligned} \begin{aligned}\\ &I_{AB}=I_{BC}=\frac{\pi \cdot 0,1^4}{32}=9,82\cdot 10^{-6}\ m^4\\ &I_{CD}=\frac{\pi \cdot 0,05^4}{32}=6,14\cdot 10^{-7}\ m^4\\ \\ &\varphi_C=\varphi_{AB}+\varphi_{BC}\\ &\varphi_C=\int\limits_{0}^{1} \frac{3,72\cdot 10^3}{80\cdot 10^9\cdot 9,82\cdot 10^{-6}}dx+\int\limits_{0}^{1} \frac{0,72\cdot 10^3}{80\cdot 10^9\cdot 9,82\cdot 10^{-6}}dx=4,74\cdot 10^{-3}+9,16\cdot 10^{-4}=5,66\cdot 10^{-3}\ rad\\ &5,66\cdot 10^{-3}\ rad=5,66\cdot 10^{-3}\cdot \frac{180}{\pi} [^o] =0,32^o\\ \end{aligned}Gráficos
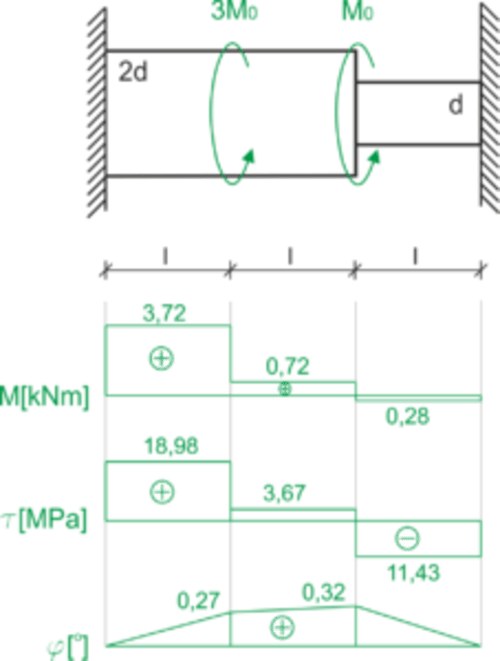
Fuente:
Niezgodziński Michał E., Tadeusz Niezgodziński, Zadania z wytrzymałości materiałów, WNT, Warszawa 2002, Przykład 5.10 s. 69
