La figura tiene dos ejes de simetría, por lo que el centro de gravedad se encuentra en su intersección. Por lo tanto, los ejes y y z marcados son los ejes principales centrales.

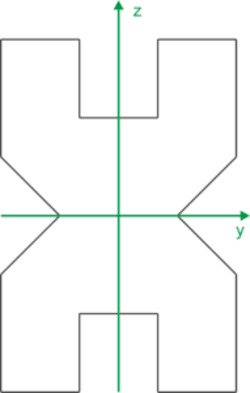
Calculamos los momentos de inercia principales centrales.

\begin{aligned} &I_{YC}=\frac{12\cdot18^3}{12}-4\frac{3^4}{12}-2\cdot\Bigg[ \frac{4^4}{12}+4\cdot4\cdot(9-2)^2 \Bigg]=4194,33cm^4\\ &I_{ZC}=\frac{18\cdot12^3}{12}-2\Bigg[ \frac{3^3\cdot6}{36}+\frac{1}{2}\cdot3\cdot6\cdot(6-1)^2 \Bigg] - 2\cdot\frac{4^4}{12}=2090,33cm^4\\ \end{aligned}