MÉTODO DEL PROCEDIMIENTO - método de fuerzas

SSN=4-3=1

Configuración básica del método de fuerzas (CBMF)

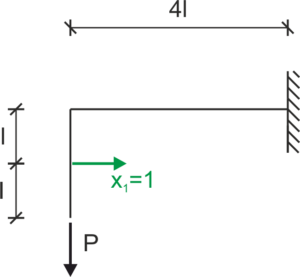
Estado \(X_1=1\)

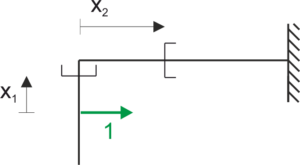
Función de momento flector

\begin{aligned} &x_{1} \in(0 ; l) \\ &M_{1}\left(x_{1}\right)=-1 \cdot x_{1} \\ &x_{2} \in(0 ; 4 l) \\ &M_{1}\left(x_{2}\right)=-l \end{aligned}

Estado P

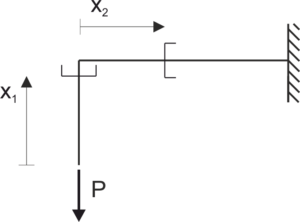
Función de momento flector

\begin{aligned} &x_{1} \in(0 ; 2 l) \\ &M_{p}\left(x_{1}\right)=0 \\ &x_{2} \in(0 ; 4 l) \\ &M_{p}\left(x_{2}\right)=-P \cdot x_{2} \end{aligned}

Ecuación canónica del método de fuerzas

\begin{gathered} \delta_{11} \cdot x_{1}+\delta_{1 p}=0 \\ E I \delta_{11}=\int_{0}^{L}\left(M_{1} \cdot M_{1}\right) d x=\int_{0}^{l} x^{2} d x+\int_{0}^{4 l} l^{2} d x=\frac{1}{3} l^{3}+4 l^{3}=\frac{13}{3} l^{3} \\ \delta_{11}=\frac{13}{3 E I} l^{3} \\ E I \delta_{1 p}=\int_{0}^{L}\left(M_{1} \cdot M_{p}\right) d x=\int_{0}^{4 l} P l x d x=P l \cdot \frac{1}{2} \cdot(4 l)^{2}=8 P l^{3} \\ \delta_{1 p}=\frac{8 P l^{3}}{E I} \\ x_{1}=\frac{-8 P l^{3}}{\frac{13}{3} l^{3}}=\frac{-24}{13} P \end{gathered}

Después de calcular la reacción estáticamente indeterminada, calculamos y dibujamos los gráficos finales.

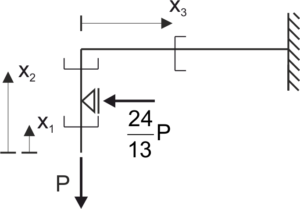\begin{aligned} &x_{1} \in(0 ; l) \\ &N\left(x_{1}\right)=P \\ &T\left(x_{1}\right)=0 \\ &M\left(x_{1}\right)=0 \\ &x_{2} \in(l ; 2 l) \\ &N\left(x_{2}\right)=P \\ &T\left(x_{2}\right)=\frac{24}{13} P \\ &M\left(x_{2}\right)=\frac{24}{13} P\left(x_{2}-l\right) \\ &M(l)=0 \\ &x_{3} \in(0 ; 4 l) \\ &N\left(x_{3}\right)=\frac{24}{13} P \\ &T\left(x_{3}\right)=-P \\ &M\left(x_{3}\right)=-\frac{28}{13} P l+P x \\ &M(0)=-\frac{28}{13} P l\\ &\quad M(2 l)=\frac{24}{13} P l \end{aligned}

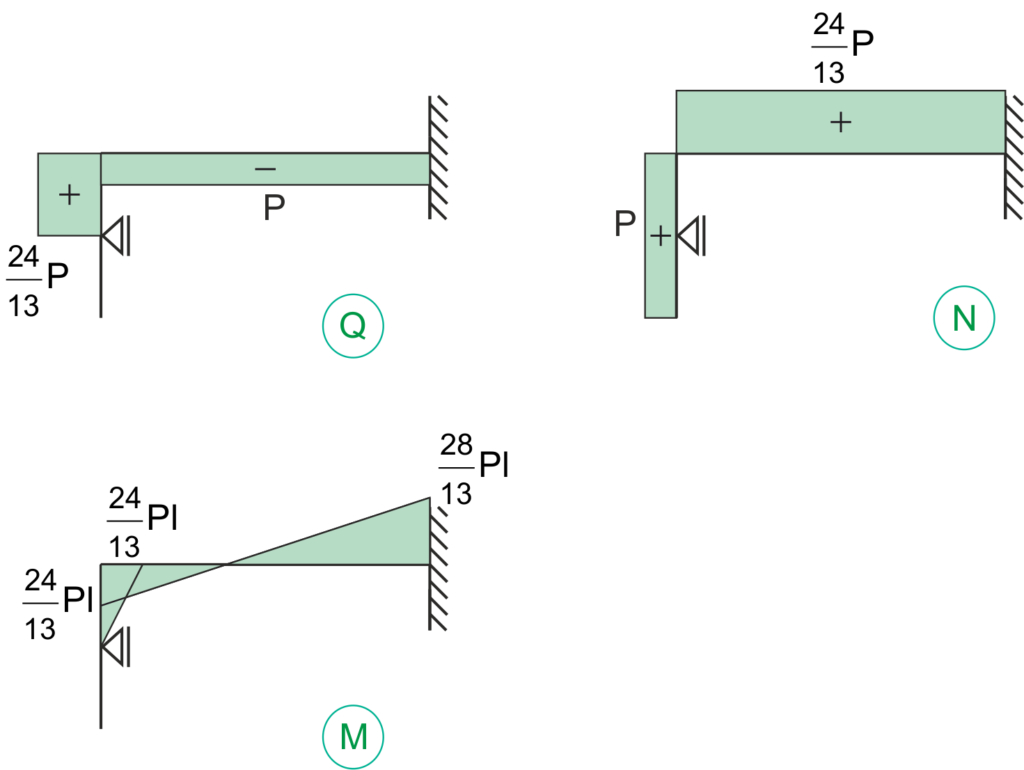
Gráficos finales de las fuerzas internas