Conversion of torque according to the formula \(M_s=9550\cdot \frac{N [kW]}{n [rpm]} M_s=9550\cdot \frac{10}{955}=100 Nm\)

The force F on the arm of half a pulley receives the torque that is applied by the engine at the beginning of the shaft. Torque occurs between the engine and the pulley. We calculate the force F on the pulley.

\begin{aligned} &F\cdot 0.2=100\Rightarrow F=500 N\\ \end{aligned}

We are dealing with bending of the shaft in one plane and torsion.

Torque diagram and bending torque calculation diagram.

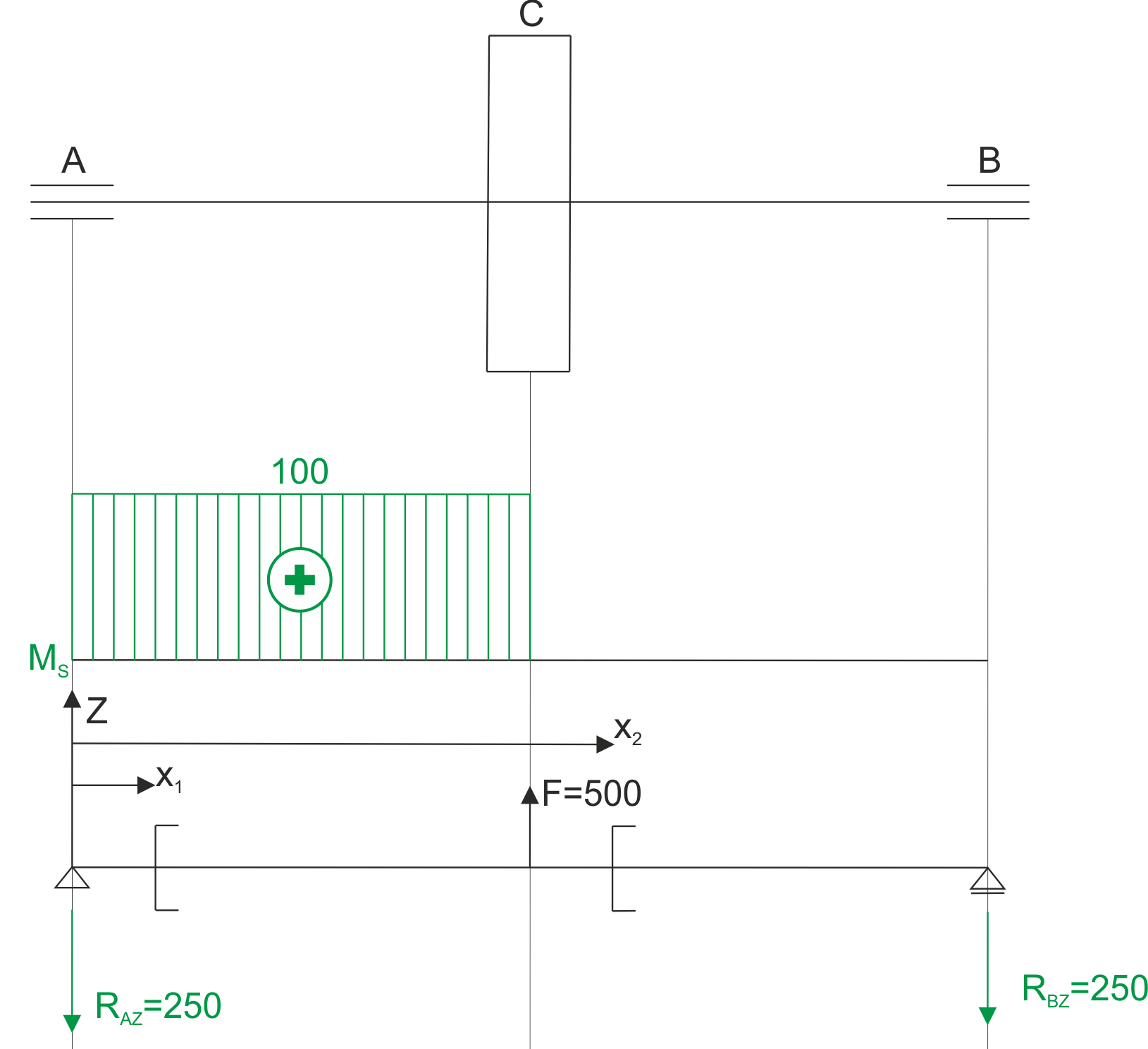\begin{aligned} &x_{1} \in(0 ; 0.5) \\ &M\left(x_{1}\right)=-R_{A Z} \cdot x_{1} \\ &M(0)=0 N m \\ &M(0.5)=-125 N m \\ &x_{2} \in(0.5 ; 1) \\ &M\left(x_{1}\right)=-R_{A Z} \cdot x_{2}+500 \cdot\left(x_{2}-0.5\right) \\ &M(0.5)=-125 N m \\ &M(1)=0 N m \end{aligned}

Bending moment diagram.

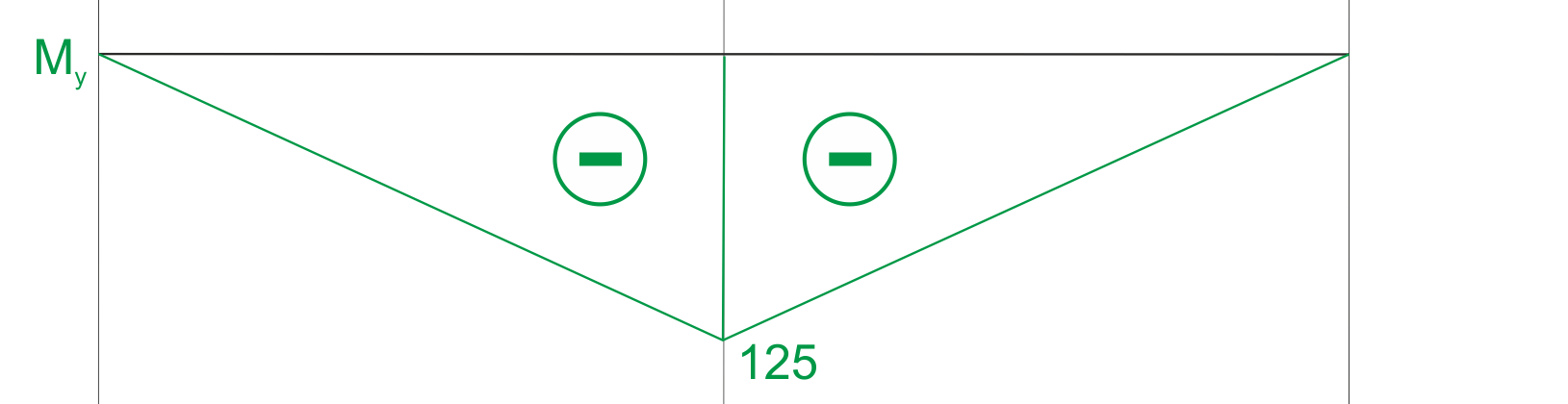
We calculate the value of the equivalent moment at characteristic points.

\begin{aligned} &M_{z a s}=\sqrt{M_{g}^{2}+\frac{3}{4} M_{s}^{2}} \\ &M_{z a s}^{A}=\sqrt{0^{2}+\frac{3}{4} \cdot 100^{2}}=86.6 \mathrm{Nm} \\ &M_{z a s}^{C A}=\sqrt{125^{2}+\frac{3}{4} \cdot 100^{2}}=152.1 \mathrm{Nm} \\ &M_{z a s}^{C B}=\sqrt{125^{2}+\frac{3}{4} \cdot 0^{2}}=125 \mathrm{Nm} \\ &M_{z a s}^{B}=\sqrt{0^{2}+\frac{3}{4} \cdot 0^{2}}=0 \mathrm{Nm} \end{aligned}

Equivalent moment diagram

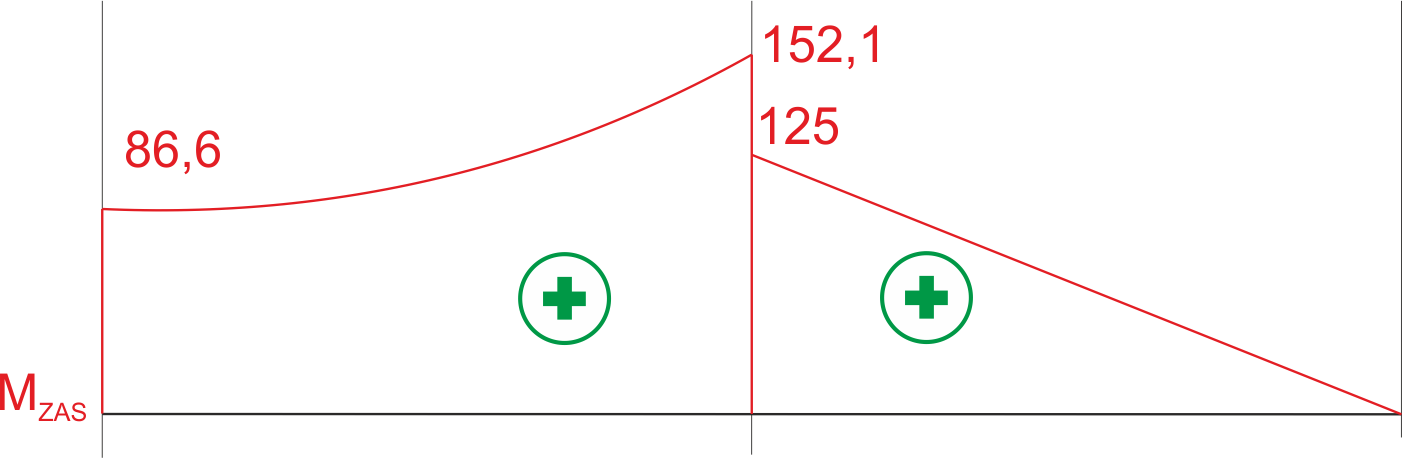
We dimension the shaft for the maximum equivalent moment. We use the derived formula

\begin{aligned} &M_{z a s}^{\max }=152.1 \mathrm{Nm} \\ &d \geq \sqrt[3]{\frac{32 M_{z a s}}{\pi \cdot k_{g}}} \\ &d \geq 0.0295 \mathrm{~m} \\ &d=3 \mathrm{~cm} \end{aligned}